【题目】为控制禽流感病毒传播,某地关闭活禽交易市场,冷冻鸡肉销量上升,某公司在春节期间采购冷冻鸡肉60箱销往城市和乡镇,已知冷冻鸡肉在城市销售平均每箱的利润y1(百元)与销售数量x(箱)的关系为y1= 在乡镇销售平均每箱的利润y2(百元)与销售数量t(箱)的关系为y2=
在乡镇销售平均每箱的利润y2(百元)与销售数量t(箱)的关系为y2=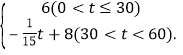
(1)t与x的关系是 ,将y2转换为x为自变量的函数,则y2= ;
(2)设春节期间售完全部冷冻鸡肉可获得总利润W(百元),当在城市销售量x(箱)的范围是0<x≤20时,求W与x的关系式(总利润=在城市销售利润+在乡镇销售利润);
(3)经测算,在20<x≤30的范围内,可以获得最大总利润,求这个最大总利润,并求出此时x的值.
参考答案:
【答案】(1)t=60-x 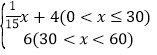 (2)W=
(2)W=![]() x2+5x+240; (3) 382.5百元
x2+5x+240; (3) 382.5百元
【解析】(1)直接利用采购冷冻鸡肉60箱销往城市和乡镇,表示出t与x的关系即可,进而代入y2求出即可;
(2)利用(1)中所求结合自变量取值范围得出W与x的函数关系式即可;
(3)利用(1)中所求结合自变量取值范围得出W与x的函数关系式,进而利用函数增减性求出函数最值即可.
(1)∵某公司在春节期间采购冷冻鸡肉60箱销往城市和乡镇,在城市销售数量x(箱),
∴在乡镇销售数量t(箱)的关系为:t=60-x,
∴y2=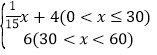 ,
,
故答案为:t=60-x,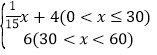 ;
;
(2)综合y1=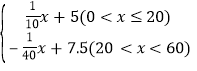 和(1)中 y2,当对应的x范围是0<x≤20 时,
和(1)中 y2,当对应的x范围是0<x≤20 时,
W=![]() x+
x+![]() (60-x)=
(60-x)=![]() x2+5x+240;
x2+5x+240;
(3)当20<x≤30时,
W=![]() x+
x+![]() (60-x)=-
(60-x)=-![]() x2+7.5x+240,
x2+7.5x+240,
∵x=-![]() =
=![]() >30,
>30,
∴在20<x≤30的范围内W随x的增大而增大,
∴当x=30时,W有最大值,W最大=-![]() ×302+7.5×30+240=382.5(百元).
×302+7.5×30+240=382.5(百元).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,图①中△ABC是等边三角形,其边长是3,图②中△DEF是等腰直角三角形,∠F=90°,DF=EF=3.
(1)若S1为△ABC的面积,S2为△DEF的面积,S3=
 AB·BC·sinB,S4=
AB·BC·sinB,S4= DE·DF·sinD,请通过计算说明S1与S3,S2与S4之间有着怎样的关系;
DE·DF·sinD,请通过计算说明S1与S3,S2与S4之间有着怎样的关系;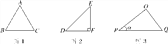
(2)在图③中,∠P=α(α为锐角),OP=m,PQ=n,△OPQ的面积为S,请你根据第(1)小题的解答,直接写出S与m,n以及α之间的关系式,并给出证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠BAC=54°,以AB为直径的⊙O分别交AC,BC于点D,E,过点B作⊙O的切线,交AC的延长线于点F.

(1)求证:BE=CE;
(2)求∠CBF的度数;
(3)若AB=6,求 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】下面选项中符合代数式书写要求的是 ( )
A.
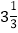 y2 B. ay·3 C.
y2 B. ay·3 C. 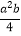 D. a×b+c
D. a×b+c -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:关于x的方程x2-2(m+1)x+m2=0.
(1)当m取何值时,方程有两个实数根?
(2)为m选取一个合适的整数,使方程有两个不相等的实数根,并求这两个根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=x2﹣(2k+1)x+k2+k(k>0)
(1)当k= 时,将这个二次函数的解析式写成顶点式;
时,将这个二次函数的解析式写成顶点式;
(2)求证:关于x的一元二次方程x2﹣(2k+1)x+k2+k=0有两个不相等的实数根. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2-(m+2)x+(2m-1)=0。
(1)求证:方程恒有两个不相等的实数根;
(2)若此方程的一个根是1,请求出方程的另一个根,并求以此两根为边长的直角三角形的周长。
相关试题

