【题目】如图1,抛物线C:y=x2经过变化可得到抛物线C1:y1=a1x(x﹣b1),C1与x轴的正半轴交与点A1 , 且其对称轴分别交抛物线C,C1于点B1 , D1 , 此时四边形OB1A1D1恰为正方形;按上述类似方法,如图2,抛物线C1:y1=a1x(x﹣b1)经过变换可得到抛物线C2:y2=a2x(x﹣b2),C2与x轴的正半轴交与点A2 , 且其对称轴分别交抛物线C1 , C2于点B2 , D2 , 此时四边形OB2A2D2也恰为正方形;按上述类似方法,如图3,可得到抛物线C3:y3=a3x(x﹣b3)与正方形OB3A3D3 . 请探究以下问题: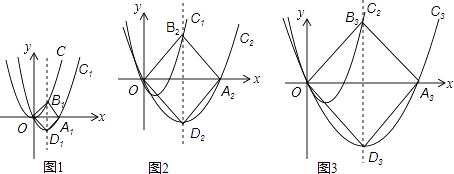
(1)填空:a1= , b1=;
(2)求出C2与C3的解析式;
(3)按上述类似方法,可得到抛物线Cn:yn=anx(x﹣bn)与正方形OBnAnDn(n≥1).
①请用含n的代数式直接表示出Cn的解析式;
②当x取任意不为0的实数时,试比较y2015与y2016的函数值的大小并说明理由.
参考答案:
【答案】
(1)1;2
(2)
解:y2=0时,a2x(x﹣b2)=0,
x1=0,x2=b2,
∴A2(b2,0),
由正方形OB2A2D2得:OA2=B2D2=b2,
∴B2( ![]() ,
, ![]() ),
),
∵B2在抛物线c1上,则 ![]() =(
=( ![]() )2﹣2×
)2﹣2× ![]() ,
,
b2(b2﹣6)=0,
b2=0(不符合题意),b2=6,
∴D2(3,﹣3),
把D2(3,﹣3)代入C2的解析式:﹣3=3a2(3﹣6),a2= ![]() ,
,
∴C2的解析式:y2= ![]() x(x﹣6)=
x(x﹣6)= ![]() x2﹣2x,
x2﹣2x,
y3=0时,a3x(x﹣b3)=0,
x1=0,x2=b3,
∴A3(b3,0),
由正方形OB3A3D3得:OA3=B3D3=b3,
∴B3( ![]() ,
, ![]() ),
),
∵B3在抛物线C2上,则 ![]() =
= ![]() (
( ![]() )2﹣2×
)2﹣2× ![]() ,
,
b3(b3﹣18)=0,
b3=0(不符合题意),b3=18,
∴D3(9,﹣9),
把D3(9,﹣9)代入C3的解析式:﹣9=9a3(9﹣18),a3= ![]() ,
,
∴C3的解析式:y3= ![]() x(x﹣18)=
x(x﹣18)= ![]() ﹣2x;
﹣2x;
(3)
解:①Cn的解析式:yn= ![]() x2﹣2x(n≥1).
x2﹣2x(n≥1).
②由上题可得抛物线C2015的解析式为:y2015= ![]() x2﹣2x,
x2﹣2x,
抛物线C2016的解析式为:y2016= ![]() x2﹣2x,
x2﹣2x,
∴两抛物线的交点为(0,0);
∴当x<0时,y2015<y2016;当x>0时,y2015>y2016.
【解析】解:(1)y1=0时,a1x(x﹣b1)=0,
x1=0,x2=b1 ,
∴A1(b1 , 0),
由正方形OB1A1D1得:OA1=B1D1=b1 ,
∴B1( ![]() ,
, ![]() ),D1(
),D1( ![]() ,﹣
,﹣ ![]() ),
),
∵B1在抛物线c上,则 ![]() =
= ![]() ,
,
b1(b1﹣2)=0,
b1=0(不符合题意),b1=2,
∴D1(1,﹣1),
把D1(1,﹣1)代入y1=a1x(x﹣b1)中得:﹣1=﹣a1 ,
∴a1=1,
故答案为:1,2;
(1)求与x轴交点A1坐标,根据正方形对角线性质表示出B1的坐标,代入对应的解析式即可求出对应的b1的值,写出D1的坐标,代入y1的解析式中可求得a1的值;(2)求与x轴交点A2坐标,根据正方形对角线性质表示出B2的坐标,代入对应的解析式即可求出对应的b2的值,写出D2的坐标,代入y2的解析式中可求得a2的值,写出抛物线C2的解析式;再利用相同的方法求抛物线C3的解析式;(3)①根据图形变换后二次项系数不变得出an=a1=1,由B1坐标(1,1)、B2坐标(3,3)、B3坐标(7,7)得Bn坐标(2n﹣1,2n﹣1),则bn=2(2n﹣1)=2n+1﹣2(n≥1),写出抛物线Cn解析式.②先求抛物线C2015和抛物线C2016的交点为(0,0),在交点的两侧观察图形得出y2015与y2016的函数值的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有理数a,b,c在数轴上的对应点如图所示.

(1)在空白处填入“>”或“<”:
a_____0;b_____0;c_____0;|a|_____|c|;|a|_____|b|;|-b|_____|c|.
(2)试在数轴上找出表示-a,-b,-c的点;
(3)试用“<”号将a,-a,b,-b,c,-c,0连接起来.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若把不等式组
 的解集在数轴上表示出来,则其对应的图形为
的解集在数轴上表示出来,则其对应的图形为A. 长方形 B. 线段 C. 射线 D. 直线
-
科目: 来源: 题型:
查看答案和解析>>【题目】现有A,B两种商品,买2件A商品和1件B商品用了90元,买3件A商品和2件B商品共用了160元.
(1)求A,B两种商品每件多少元?
(2)如果小亮准备购买A,B两种商品共10件,总费用不超过350元,且不低于300元,问有几种购买方案,哪种方案费用最低?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠BAC=90°,AB=AC,在△ABC的外部作∠ACM,使得∠ACM=
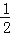 ∠ABC,点D是直线BC上的动点,过点D作直线CM的垂线,垂足为E,交直线AC于F.
∠ABC,点D是直线BC上的动点,过点D作直线CM的垂线,垂足为E,交直线AC于F.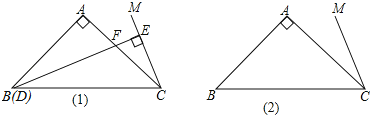
(1)如图1所示,当点D与点B重合时,延长BA,CM交点N,证明:DF=2EC;
(2)当点D在直线BC上运动时,DF和EC是否始终保持上述数量关系呢?请你在图2中画出点D运动到CB延长线上某一点时的图形,并证明此时DF与EC的数量关系.
-
科目: 来源: 题型:
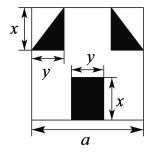
查看答案和解析>>【题目】“囧”像一个人脸郁闷的神情.如图,边长为a的正方形纸片,剪去两个一样的小直角三角形(阴影部分)和一个长方形(阴影部分)得到一个“囧”字图案,设剪去的两个小直角三角形的两直角边长分别为x、y,剪去的小长方形长和宽也分别为x,y.
(1)用含a、x、y的式子表示“囧”的面积;
(2)当a=12,x=7,y=4时,求该图形面积的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设a1=22-02,a2=32-12,…,an=(n+1)2-(n-1)2(n为大于1的整数)
(1)计算a15的值;
(2)通过拼图你发现前三个图形的面积之和与第四个正方形的面积之间有什么关系:
__________________________________(用含a、b的式子表示);
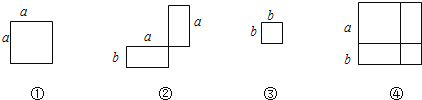
(3)根据(2)中结论,探究an=(n+1)2-(n-1)2是否为4的倍数.
相关试题

