【题目】在△ABC中,∠BAC=90°,AB=AC,在△ABC的外部作∠ACM,使得∠ACM=![]() ∠ABC,点D是直线BC上的动点,过点D作直线CM的垂线,垂足为E,交直线AC于F.
∠ABC,点D是直线BC上的动点,过点D作直线CM的垂线,垂足为E,交直线AC于F.
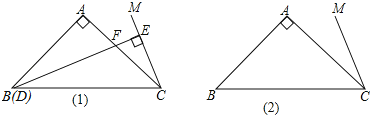
(1)如图1所示,当点D与点B重合时,延长BA,CM交点N,证明:DF=2EC;
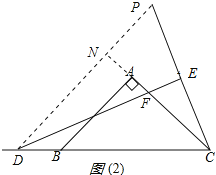
(2)当点D在直线BC上运动时,DF和EC是否始终保持上述数量关系呢?请你在图2中画出点D运动到CB延长线上某一点时的图形,并证明此时DF与EC的数量关系.
参考答案:
【答案】(1)见解析;(2)DF=2CE
【解析】
试题分析:(1)延长BA,CM交点N,先证明BC=BN,得出CN=2CE,再证明△BAF≌△CAN,得出对应边相等BF=CN,即可得出结论;
(2)作∠PDE=22.5,交CE的延长线于P点,交CA的延长线于N,先证明PD=CD,得出PC=2CE,再证明△DNF≌△PNC,得出对应边相等DF=PC,即可得出结论.
解:(1)如图(1),延长BA,CM交点N,
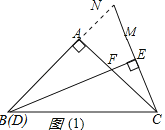
∵∠A=90°,AB=AC,
∴∠ABC=∠ACB=45°,
∵∠ACM=![]() ∠ABC=22.5°,
∠ABC=22.5°,
∴∠BCM=67.5°,
∴∠BNC=67.5°=∠BCM,
∴BC=BN,
∵BE⊥CE,
∴∠ABE=22.5°,CN=2CE,
∴∠ABE=∠ACM=22.5°,
在△BAF和△CAN中,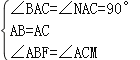 ,
,
∴△BAF≌△CAN(ASA),
∴BF=CN,
∴BF=2CE;
(2)保持上述关系;BF=2CE;
证明如下:
作∠PDE=22.5,交CE的延长线于P点,交CA的延长线于N,
如图(2)所示:
∵DE⊥PC,∠ECD=67.5,
∴∠EDC=22.5°,
∴∠PDE=∠EDC,∠NDC=45°,
∴∠DPC=67.5°,
∴PD=CD,
∴PE=EC,
∴PC=2CE,
∵∠NDC=45°,∠NCD=45°,
∴∠NCD=∠NDC,∠DNC=90°,
∴ND=NC且∠DNC=∠PNC,
在△DNF和△PNC中,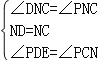 ,
,
∴△DNF≌△PNC(ASA),
∴DF=PC,
∴DF=2CE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个三角形的三边长分别为x、8、2,那么x的取值范围是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的口袋里装有若干除颜色外其他完全相同的小球,其中有6个黄球,将口袋中的球摇匀,从中任意摸出一个球记下颜色后再放回,通过大量重复上述实验后发现,摸到黄球的频率稳定在30%,由此估计口袋中共有小球 个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形的内角和等于外角和,则这个多边形是_________边形 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,“赵爽弦图”由4个全等的直角三角形拼成,在Rt△ABC中,∠ACB=90°,AC=b,BC=a,请你利用这个图形解决下列问题:
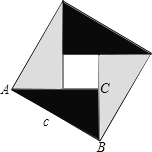
(1)证明勾股定理;
(2)说明a2+b2≥2ab及其等号成立的条件.
-
科目: 来源: 题型:
查看答案和解析>>【题目】写出命题“如果a=b”,那么“3a=3b”的逆命题 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:已知|a–4| + ( b+1 )2 = 0,求5ab2–[2a2b-(4ab2-2a2b)]+4a2b的值。
相关试题

