搜索
【题目】在风速为25 km/h的条件下，一架飞机顺风从A机场飞到B机场要用5.6h，它逆风飞行同样的航线要用6h．求：
(1)无风时这架飞机在这一航线的平均航速；
(2)两机场之间的航程是多少？
参考答案：
【答案】（1）
;（2）4200km
【解析】
（1）设无风时飞机的航速是x千米/时，根据顺风速度×顺风时间=逆风速度×逆风时间，列出方程求出x的值即可．
（2）由“航程=速度×时间”进行计算．
（1）设无风时飞机的航速是x千米/时，
依题意得：5.6×（x+25）=6×（x-25），
解得：x=725．
答：无风时飞机的航速是725千米/时．
（2）由（1）知，无风时飞机的航速是725千米/时，则
6×（725-25）=4200（千米）．
答：两机场之间的航程是4200千米．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图：在长度为1个单位的小正方形组成的网格中，点A、B、C在小正方形的顶点上．
（1）在图中画出与△ABC关于直线l成轴对称的△AB′C′;
（2）△ABC的面积为________;
（3）在直线l上找一点P，使PB+PC的长最短，则这个最短长度为________个单位长度．（在图形中标出点P）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，矩形OABC的顶点A，C分别在x轴和y轴上，点B的坐标为（4，6）．双曲线y=
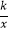（x＞0）的图象经过BC的中点D，且与AB交于点E，连接DE．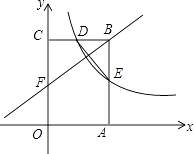
（1）求k的值及点E的坐标；
（2）若点F是边上一点，且△BCF∽△EBD，求直线FB的解析式． -
科目： 来源： 题型：
查看答案和解析>>【题目】阅读材料并解答下列问题．
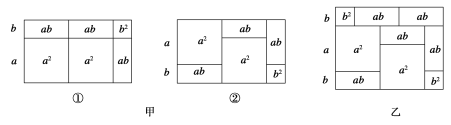
你知道吗？一些代数恒等式可以用平面图形的面积来表示，例如(2a＋b)(a＋b)＝2a2＋3ab＋b2就可以用图甲中的①或②的面积表示．
(1)请写出图乙所表示的代数恒等式；
(2)画出一个几何图形，使它的面积能表示(a＋b)(a＋3b)＝a2＋4ab＋3b2；
(3)请仿照上述式子另写一个含有a，b的代数恒等式，并画出与之对应的几何图形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，Rt△ABO中，∠OAB=Rt∠，点A在x轴的正半轴，点B在第一象限，C，D分别是BO，BA的中点，点E在CD的延长线上．若函数y1=
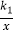（x＞0）的图象经过B，E，函数y2= 
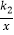（x＞0）的图象过点C，且△BCE的面积为1，则k2的值为（ ）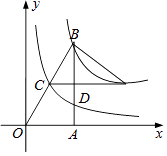 
A.
B.
C.3
D.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，P是边长为1的正方形ABCD对角线AC上一动点（P与A、C不重合），点E在射线BC上，且PE=PB．设AP=x，△PBE的面积为y．则能够正确反映y与x之间的函数关系的图象是（ ）
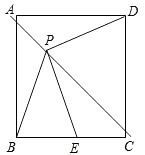
A.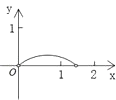
B.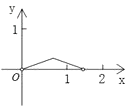
C.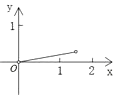
D.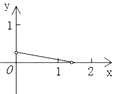
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读材料：
小明在学习二次根式的化简后，遇到了这样一个需要化简的式子：
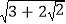．该如何化简呢？思考后，他发现3+2
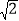=1+2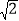+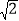（）2=（1+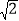）2．于是=
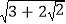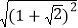=1+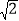．善于思考的小明继续深入探索；当a+b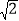=（m+n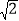）2时（其中a，b，m，n均为正整数），则a+b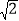=m2+2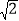mn+2n2．此时，a=m2+2n2，b=2mn，于是，
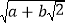=m+n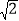．请你仿照小明的方法探索并解决下列问题：（1）设a，b，m，n均为正整数且
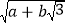=m+n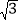
，用含m，n的式子分别表示a，b时，结果是a= ，b= ；（2）利用（1）中的结论，选择一组正整数填空：
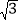= + ；（3）化简：
．
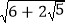相关试题
