搜索
【题目】如图，Rt△ABO中，∠OAB=Rt∠，点A在x轴的正半轴，点B在第一象限，C，D分别是BO，BA的中点，点E在CD的延长线上．若函数y1= 
（x＞0）的图象经过B，E，函数y2= 
（x＞0）的图象过点C，且△BCE的面积为1，则k2的值为（ ）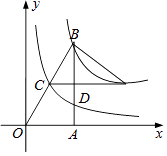 
A.
B.
C.3
D.
参考答案：
【答案】B
【解析】解：∵点C为线段OB的中点，且函数y1= 
（x＞0）的图象经过B，E，函数y2= 
（x＞0）的图象过点C， ∴k1=4k2 ．
设点C的坐标为（m， 
）（m＞0），则点B的坐标为（2m， 
），点E的坐标为（4m， ），
∴CE=3m，BD= ，
∴S△BCE= 
CEBD= ×3m× = 
k2=1，
解得：k2= 
．
故选B．
【考点精析】本题主要考查了比例系数k的几何意义的相关知识点，需要掌握几何意义：表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积才能正确解答此题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，矩形OABC的顶点A，C分别在x轴和y轴上，点B的坐标为（4，6）．双曲线y=
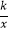（x＞0）的图象经过BC的中点D，且与AB交于点E，连接DE．
（1）求k的值及点E的坐标；
（2）若点F是边上一点，且△BCF∽△EBD，求直线FB的解析式． -
科目： 来源： 题型：
查看答案和解析>>【题目】阅读材料并解答下列问题．
你知道吗？一些代数恒等式可以用平面图形的面积来表示，例如(2a＋b)(a＋b)＝2a2＋3ab＋b2就可以用图甲中的①或②的面积表示．
(1)请写出图乙所表示的代数恒等式；
(2)画出一个几何图形，使它的面积能表示(a＋b)(a＋3b)＝a2＋4ab＋3b2；
(3)请仿照上述式子另写一个含有a，b的代数恒等式，并画出与之对应的几何图形．
-
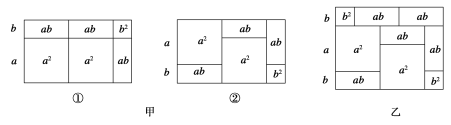
科目： 来源： 题型：
查看答案和解析>>【题目】在风速为25 km/h的条件下，一架飞机顺风从A机场飞到B机场要用5.6h，它逆风飞行同样的航线要用6h．求：
(1)无风时这架飞机在这一航线的平均航速；
(2)两机场之间的航程是多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，P是边长为1的正方形ABCD对角线AC上一动点（P与A、C不重合），点E在射线BC上，且PE=PB．设AP=x，△PBE的面积为y．则能够正确反映y与x之间的函数关系的图象是（ ）
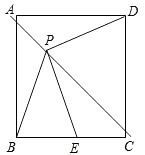
A.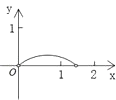
B.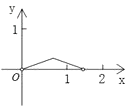
C.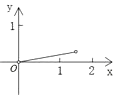
D.
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读材料：
小明在学习二次根式的化简后，遇到了这样一个需要化简的式子：
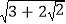．该如何化简呢？思考后，他发现3+2
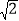=1+2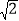+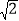（）2=（1+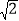）2．于是=
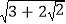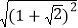=1+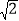．善于思考的小明继续深入探索；当a+b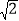=（m+n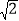）2时（其中a，b，m，n均为正整数），则a+b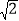=m2+2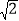mn+2n2．此时，a=m2+2n2，b=2mn，于是，
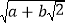=m+n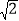．请你仿照小明的方法探索并解决下列问题：（1）设a，b，m，n均为正整数且
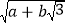=m+n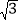
，用含m，n的式子分别表示a，b时，结果是a= ，b= ；（2）利用（1）中的结论，选择一组正整数填空：
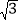= + ；（3）化简：
． -
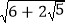科目： 来源： 题型：
查看答案和解析>>【题目】某班去体育用品商店购买羽毛球和羽毛球拍，每只羽毛球2元，每副羽毛球拍25元．甲商店说：“羽毛球拍和羽毛球都打9折优惠”，乙商店说：“买一副羽毛球拍赠2只羽毛球”．
（1）该班如果买2副羽毛球拍和20只羽毛球，问在甲、乙两家商店各需花多少钱？
（2）该班如果准备花90元钱全部用于买2副羽毛球拍和若干只羽毛球，请问到哪家商店购买更合算？
（3）该班如果必须买2副羽毛球拍，问当买多少只羽毛球时到两家商店购买同样合算？
相关试题
