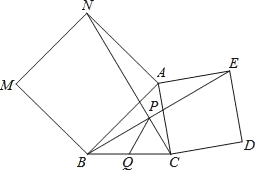
【题目】如图,分别以△ABC的两边AB和AC为边向外作正方形ANMB和正方形ACDE,NC、BE交于点P.
探究:试判断BE和CN的位置关系和数量关系,并说明理由.
应用:Q是线段BC的中点,若BC=6,则PQ= .
参考答案:
【答案】见解析
【解析】试题分析:根据正方形性质得出AN=AB,AC=AE,∠NAB=∠CAE=90°,求出∠NAC=∠BAE,证出△ANC≌△ABE即可.
试题解析:解:CN=BE,BE⊥NC.理由如下:
∵四边形ANMB和四边形ACDE都是正方形,∴AN=AB,AC=AE,∠NAB=∠CAE=90°,∴∠NAB+∠BAC=∠CAE+∠BAC,∴∠NAC=∠BAE.
在△ANC和△ABE中,∵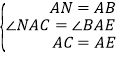 ,∴△ANC≌△ABE(SAS),∴CN=BE.
,∴△ANC≌△ABE(SAS),∴CN=BE.
设CN交AB于H,交BE于P.∵△ANC≌△ABE,∴∠ABE=∠ANC.∵∠PHB=∠AHN,∴∠HPB=∠HAP=90°,∴BE⊥NC.∵四边形NABM是正方形,∴∠NAB=90°,∴∠ANC+∠AON=90°.∵∠BHP=∠AHN,∠ANC=∠ABE,∴∠ABP+∠BHP=90°,∴∠BPC=∠ABP+∠BHP=90°.∵Q为BC中点,BC=6,∴PQ=![]() BC=3.故答案为:3.
BC=3.故答案为:3.
-
科目: 来源: 题型:
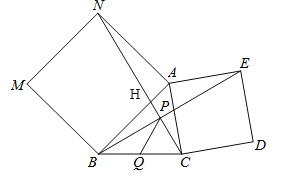
查看答案和解析>>【题目】如图 ,在平面直角坐标系中,边长为 1 的正方形OA1B1C 的对角线 A1C 和OB1 交于点 M1,以 M1A1为对角线作第二个正方形 A2A1B2M1对角线 A1M1和 A2 B2 交于点 M 2 ;以 M 2 A1 为对角线作第三个正方形 A3 A1B3M 2,对角线 A1M 2 和 A3 B3 交于点 M 3 ;…,依此类推,那么 M 1 的坐标为_____;这样作的第 n 个正方形的对角线交点 Mn 的坐标为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校积极开展“阳光体育”活动,共开设了跳绳、足球、篮球、跑步四种运动项目,为了解学生最喜爱哪一种项目,随机抽取了部分学生进行调查,并绘制了如图不完整的条形统计图和扇形统计图(部分信息未给出)
(1)求本次调查学生的人数.
(2)求喜爱足球、跑步的人数,并补全条形统计图;
(3)求喜爱篮球、跑步的人数占调查人数的百分比.

-
科目: 来源: 题型:
查看答案和解析>>【题目】华联超市第一次用7000元购进甲、乙两种商品,其中甲商品的件数是乙商品件数的2倍,甲、乙两种商品的进价和售价如表:(注:获利=售价﹣进价)
甲
乙
进价(元/件)
20
30
售价(元/件)
25
40
(1)该超市购进甲、乙两种商品各多少件?
(2)该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(3)该超市第二次以第一次的进价又购进甲、乙两种商品,其中甲商品的件数不变,乙商品的件数是第一次的3倍:甲商品按原价销售,乙商品打折销售,第二次两种商品都售完以后获得的总利润比第一次获得的总利润多800元,求第二次乙商品是按原价打几折销售?
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义一种对正整数n的“F”运算:①当n为奇数时,F(n)=3n+1;②当n为偶数时,F(n)=
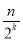 (其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=24,则:若n=13,则第2018次“F”运算的结果是_____.
(其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=24,则:若n=13,则第2018次“F”运算的结果是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于每个正整数 n,关于 x 的一元二次方程
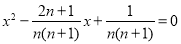 0 的两个根分别为 an、bn,设平面直角坐标系中,An、Bn 两点的坐标分别为 An(an,0),Bn(bn,0),AnBn 表示这两点间的距离,则 AnBn=____________(用含 n 的代数式表示);A1B1+ A2B2+ …+ A2011B2012 的值为______.
0 的两个根分别为 an、bn,设平面直角坐标系中,An、Bn 两点的坐标分别为 An(an,0),Bn(bn,0),AnBn 表示这两点间的距离,则 AnBn=____________(用含 n 的代数式表示);A1B1+ A2B2+ …+ A2011B2012 的值为______. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上每相邻两点的相距一个单位长度,点A、B、C、D是这些点中的四个,且对应的位置如图所示,它们对应的数分别是a,b,c,d.
(1)当ab=﹣1,则d= .
(2)若|d﹣2a|=7,求点C对应的数.
(3)若abcd<0,a+b>0,化简|a﹣b|﹣|b+c﹣5|﹣|c﹣5|﹣|d﹣a|+|8﹣d|.

相关试题

