【题目】如图,等腰Rt△ABC中,∠ACB=90°,AC=BC,点D、E分别在边AB、CB上,CD=DE,∠CDB=∠DEC,过点C作CF⊥DE于点F,交AB于点G,
(1)求证:△ACD≌△BDE;
(2)求证:△CDG为等腰三角形.

参考答案:
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)根据题意和图形,利用全等三角形的判定可以证明结论成立;
(2)根据题意和(1)中的结论,利用全等三角形的性质和等腰三角形的判定可以证明结论成立.
证明:(1)∵∠CDB=∠DEC,
∴∠ADC=∠BED,
∵AC=BC,
∴∠A=∠B,
在△ACD与△BDE中,
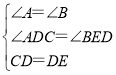 ,
,
∴△ACD≌△BDE(AAS);
(2)由(1)知,△ACD≌△BDE,
∴∠ACD=∠BDE,
∵在Rt△ACB中,AC=BC,
∴∠A=∠B=45°,
∴∠CDG=45°+∠ACD,∠DGC=45°+∠BCG,
∴∠CDF=45°,
∵CF⊥DE交BD于点G,
∴∠DFC=90°,
∴∠DCF=45°,
∵DC=DE,
∴∠DCE=∠DEC,
∵∠DCE=∠DCF+∠BCG=45°+∠BCG,∠DEC=∠B+∠BDE=45°+∠BDE,
∴∠BCG=∠BDE,
∴∠ACD=∠BCG,
∴∠CDG=∠CGD,
∴CD=CG,
∴△CDG是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个四位数,记千位数字与百位数字之和为x,十位数字与个位数字之和为y,如果x=y,那么称这个四位数为“平衡数”.
(1)最小的“平衡数”为 ;四位数A与4738之和为最大的“平衡数”,则A的值为_______;
(2)一个四位“平衡数”M,它的个位数字是千位数字a的3倍,百位数字b与十位数字之和为8,求出所有满足条件的“平衡数”M的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为半圆O的直径,以AO为直径作半圆M,C为OB的中点,D在半圆M上,且CD⊥MD,延长AD交半圆O于点E,且AB=4,则圆中阴影部分的面积为_____________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在等腰△ABC中,AB=AC=
 ,BC=4,点D从A出发以每秒
,BC=4,点D从A出发以每秒 个单位的速度向点B运动,同时点E从点B出发以每秒4个单位的速度向点C运动,在DE的右侧作∠DEF=∠B,交直线AC于点F,设运动的时间为t秒,则当△ADF是一个以AD为腰的等腰三角形时,t的值为_____.
个单位的速度向点B运动,同时点E从点B出发以每秒4个单位的速度向点C运动,在DE的右侧作∠DEF=∠B,交直线AC于点F,设运动的时间为t秒,则当△ADF是一个以AD为腰的等腰三角形时,t的值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,△ABC是等边三角形,D是边BC上的任意一点,∠ADF=60°,且DF交∠ACE的角平分线于点F.


(1)求证:AC=CD+CF;
(2)如图2,当点D在BC的延长上时,猜想AC、CD、CF的数量关系,并证明你的猜想.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面坐标系中,ΔABC是等腰直角三角形,∠ABC=90°,AB=BC,点A坐标为(-8,-3),点B坐标为(0,-5),AC交x轴于点D.

(1)求点C和D的坐标;
(2)点M在x轴上,当ΔAMB的周长最小时,求点M的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,
, ,
, .点
.点 从点
从点 出发,沿折线
出发,沿折线 —
— 以每秒1个单位长度的速度向终点
以每秒1个单位长度的速度向终点 运动,点
运动,点 从点
从点 出发沿折线
出发沿折线 -
- 以每秒3个单位长度的速度向终点
以每秒3个单位长度的速度向终点 运动,
运动, 、
、 两点同时出发.分别过
两点同时出发.分别过 、
、 两点作
两点作 于
于 ,
, 于
于 .设点
.设点 的运动时间为
的运动时间为 (秒).
(秒).
(1)当
 、
、 两点相遇时,求
两点相遇时,求 的值.
的值.(2)在整个运动过程中,求
 的长(用含
的长(用含 的代数式表示).
的代数式表示).(3)当
 与
与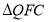 全等时,直接写出所有满足条件的
全等时,直接写出所有满足条件的 的长.
的长.
相关试题

