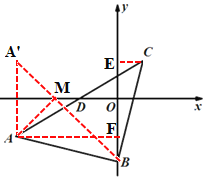
【题目】如图,在平面坐标系中,ΔABC是等腰直角三角形,∠ABC=90°,AB=BC,点A坐标为(-8,-3),点B坐标为(0,-5),AC交x轴于点D.

(1)求点C和D的坐标;
(2)点M在x轴上,当ΔAMB的周长最小时,求点M的坐标.
参考答案:
【答案】(1)C(2,3),D(-3,0);(2)M(-5,0).
【解析】
(1)分别作AF⊥y轴,CE⊥y轴,垂足为F,E,证明△AFB≌△CEB,得BE=AF=8,CE=BF=2,又OB=5,从而可得点C 的坐标,设AC的直线解析式为y=kx+b,把A,C点的坐标分别代入直线解析式,求出k和b的值,令y=0,求出x的值即可;
(2)作A点关于x轴的对称点A‘,连接A’B交x轴于点M,此时ΔAMB的周长最小,设直线A’B的解析式为y=ax+b,把A’,B点的坐标分别代入,求出其解析式,令y=0,求出x的值即可.
(1)分别作AF⊥y轴,CE⊥y轴,垂足为F,E,
∴∠AFB=∠BEC=90°,
∴∠BAF+∠ABF=90°, ∠CBE+∠BCE=90°,
∵∠ABF+∠CBE=∠ABC=90°
∴∠ABF=∠BCE,
∵AB=BC,
∴△ABF≌△BCE,
∴BE=AF,CE=BF
∵A(-8,-3),B(0,-5),
∴AF=8,OF=3,OB=5,
∴OE=3,CE=2,
∴C点坐标为(2,3);
设直线AC的关系式为y=kx+b,把A(-8,-3),C(2,3)分别代入得,
![]() ,
,
解得,![]() ,
,
所以,直线AC的解析式为:![]() ,
,
令y=0,则有![]() ,解得,x=-3,
,解得,x=-3,
∴D点坐标为(-3,0);
(2)如图,作A点关于x轴的对称点A‘,连接A’B交x轴于点M,此时ΔAMB的周长最小,
设直线A’B的解析式为y=ax+b,把A’(-8,3),B(0,-5)分别代入解析式得,
![]() ,
,
解得,![]()
所以,直线A’B的解析式为:y=-x-5,
令y=0,则x=-5,
所以,M点的坐标为(-5,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在等腰△ABC中,AB=AC=
 ,BC=4,点D从A出发以每秒
,BC=4,点D从A出发以每秒 个单位的速度向点B运动,同时点E从点B出发以每秒4个单位的速度向点C运动,在DE的右侧作∠DEF=∠B,交直线AC于点F,设运动的时间为t秒,则当△ADF是一个以AD为腰的等腰三角形时,t的值为_____.
个单位的速度向点B运动,同时点E从点B出发以每秒4个单位的速度向点C运动,在DE的右侧作∠DEF=∠B,交直线AC于点F,设运动的时间为t秒,则当△ADF是一个以AD为腰的等腰三角形时,t的值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰Rt△ABC中,∠ACB=90°,AC=BC,点D、E分别在边AB、CB上,CD=DE,∠CDB=∠DEC,过点C作CF⊥DE于点F,交AB于点G,
(1)求证:△ACD≌△BDE;
(2)求证:△CDG为等腰三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,△ABC是等边三角形,D是边BC上的任意一点,∠ADF=60°,且DF交∠ACE的角平分线于点F.


(1)求证:AC=CD+CF;
(2)如图2,当点D在BC的延长上时,猜想AC、CD、CF的数量关系,并证明你的猜想.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,
, ,
, .点
.点 从点
从点 出发,沿折线
出发,沿折线 —
— 以每秒1个单位长度的速度向终点
以每秒1个单位长度的速度向终点 运动,点
运动,点 从点
从点 出发沿折线
出发沿折线 -
- 以每秒3个单位长度的速度向终点
以每秒3个单位长度的速度向终点 运动,
运动, 、
、 两点同时出发.分别过
两点同时出发.分别过 、
、 两点作
两点作 于
于 ,
, 于
于 .设点
.设点 的运动时间为
的运动时间为 (秒).
(秒).
(1)当
 、
、 两点相遇时,求
两点相遇时,求 的值.
的值.(2)在整个运动过程中,求
 的长(用含
的长(用含 的代数式表示).
的代数式表示).(3)当
 与
与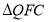 全等时,直接写出所有满足条件的
全等时,直接写出所有满足条件的 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O且AB=AC,延长BC至点D,使CD=CA,连接AD交⊙O于点E,连接BE、CE.
(1)求证:△ABE≌△CDE;
(2)填空:
①当∠ABC的度数为 时,四边形AOCE是菱形;
②若AE=6,EF=4,DE的长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在已知的△ABC中,按以下步骤作图:①分别以B,C为圆心,以大于
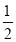 BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD.若CD=AC,∠A=50°,则∠ACB的度数为( )
BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD.若CD=AC,∠A=50°,则∠ACB的度数为( ) 
A. 90°B. 95°C. 100°D. 105°
相关试题

