【题目】如图所示,在等边三角形ABC中,BC=8cm,射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设运动时间为t(s).
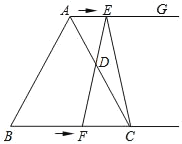
(1)连接EF,当EF经过AC边的中点D时,求证:四边形AFCE是平行四边形;
(2)填空:①当t为 s时,四边形ACFE是菱形;②当t为 s时,△ACE的面积是△ACF的面积的2倍.
参考答案:
【答案】(1)见解析;
(2)①8;②t=![]() 或y=
或y=![]() .
.
【解析】
(1)判断出△ADE≌△CDF得出AE=CF,即可得出结论;
(2)①先求出AC=BC=8,进而判断出AE=CF=AC=8,即可得出结论;
②先判断出△ACE和△ACF的边AE和CF上的高相等,进而判断出AE=2CF,再分两种情况,建立方程求解即可得出结论.
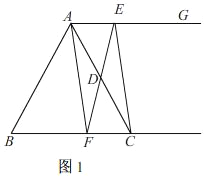
解:(1)如图1.
∵AG∥BC,
∴∠EAC=∠FCA,∠AED=∠CFD.
∵EF经过AC边的中点D,
∴AD=CD,
∴△ADE≌△CDF(AAS),
∴AE=CF.
∵AE∥FC,
∴四边形AFCE是平行四边形;
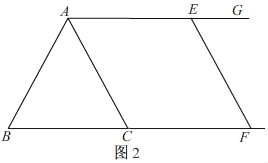
(2)①如图2.
∵△ABC是等边三角形,
∴AC=BC=8.
∵四边形ACFE是菱形,
∴AE=CF=AC=BC=8,且点F在BC延长线上,由运动知,AE=t,BF=2t,
∴CF=2t﹣8,t=8,将t=8代入CF=2t﹣8中,
得CF=8=AC=AE,符合题意,即:t=8秒时,四边形ACFE是菱形.
故答案为:8;
②设平行线AG与BC的距离为h,
∴△ACE边AE上的高为h,△ACF的边CF上的高为h.
∵△ACE的面积是△ACF的面积的2倍,
∴AE=2CF,当点F在线段BC上时(0<t<4),CF=8﹣2t,AE=t,
∴t=2(8﹣2t),
∴![]()
当点F在BC的延长线上时(t>4),CF=2t﹣8,AE=t,
∴t=2(2t﹣8),
∴![]()
即:t=![]() 秒或
秒或![]() 秒时,△ACE的面积是△ACF的面积的2倍.
秒时,△ACE的面积是△ACF的面积的2倍.
故答案为:![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形AEFG的顶点E,G分别在正方形ABCD的AB,AD边上,连接B,交EF于点M,交FG于点N,设AE=a,AG=b,AB=c(b<a<c).
(1)求证:
 ;
;(2)求△AMN的面积(用a,b,c的代数式表示);
(3)当∠MAN=45°时,求证:c2=2ab.

-
科目: 来源: 题型:
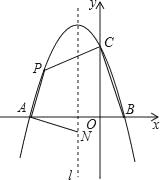
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c与x轴交于点A和点B(1,0),与y轴交于点C(0,3),其对称轴l为x=﹣1.
(1)求抛物线的解析式并写出其顶点坐标;
(2)若动点P在第二象限内的抛物线上,动点N在对称轴l上.
①当PA⊥NA,且PA=NA时,求此时点P的坐标;
②当四边形PABC的面积最大时,求四边形PABC面积的最大值及此时点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,
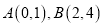 ,将线段
,将线段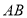 平移得到线段
平移得到线段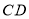 ,点
,点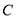 的坐标为
的坐标为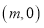 ,连结
,连结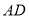 .
.(1)点
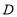 的坐标为__________________(用含
的坐标为__________________(用含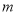 的式子表示);
的式子表示);(2)若
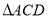 的面积为4,求点
的面积为4,求点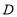 的坐标;
的坐标;(3)如图2,在(2)的条件下,延长
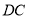 交
交 轴于点
轴于点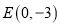 ,延长
,延长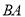 交
交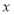 轴于
轴于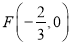 ,
, 是
是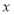 轴上一动点,
轴上一动点,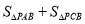 的值记为
的值记为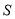 ,在点
,在点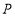 运动的过程中,
运动的过程中,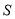 的值是否发生变化,若不变,请求出
的值是否发生变化,若不变,请求出 的值,并写出此时
的值,并写出此时 的取值范围,若变化,说明理由.
的取值范围,若变化,说明理由.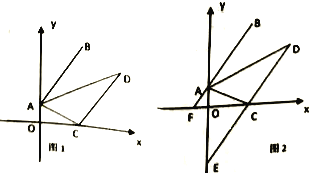
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,BM是∠ABC的平分线,交CD于点M,且DM=2,平行四边形ABCD的周长是14,则BC的长等于( )

A. 2B. 2.5C. 3D. 3.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,
 ,
, 分别在直线
分别在直线 上,
上, 是平面内一点,
是平面内一点, 和
和 的平分线所在直线相交于点
的平分线所在直线相交于点 .
.(1)如图1,当
 都在直线
都在直线 之间,且
之间,且 时,
时, 的度数为_________;
的度数为_________;(2)如图2,当
 都在直线
都在直线 上方时,探究
上方时,探究 和
和 之间的数量关系,并证明你的结论;
之间的数量关系,并证明你的结论;(3)如图3,当
 在直线
在直线 两侧时,直接写出
两侧时,直接写出 和
和 之间的数量关系是_____.
之间的数量关系是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠CAB=2∠B,AE平分∠CAB,CD⊥AB于D,AC=3,AD=1.下列结论:①∠AEC=∠CAB;②EF=CE;③AC=AE;④BD=4;

正确的是___________(填序号)
相关试题

