搜索
【题目】为了倡导“节约用水，从我做起”，市政府决定对市直机关500户家庭的用水情况作一次调查，市政府调查小组随机抽查了其中100户家庭一年的月平均用水量（单位：吨）．并将调查结果绘制成了如图所示的条形统计图，则这组数据的众数和中位数分别是（ ）
A.40，20
B.11，11
C.11，12
D.11，11.5
参考答案：
【答案】D
【解析】解：由条形图知，约平均用水量最多的是11吨，即众数为11；
100个数据的中位数为第50、51个数据的平均数，即中位数为 
=11.5，
所以答案是：D．
【考点精析】本题主要考查了中位数、众数的相关知识点，需要掌握中位数是唯一的，仅与数据的排列位置有关，它不能充分利用所有数据；众数可能一个，也可能多个，它一定是这组数据中的数才能正确解答此题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：AB是⊙O的直径，BD是⊙O的弦，延长BD到点C，使AB=AC，连结AC，过点D作DE⊥AC，垂足为E．
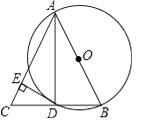
（1）求证：DC=BD；
（2）求证：DE为⊙O的切线． -
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，已知抛物线经过A（﹣4，0），B（0，﹣4），C（2，0）三点．
（1）求抛物线的解析式；
（2）若点M为第三象限内抛物线上一动点，点M的横坐标为m，△AMB的面积为S．求S关于m的函数关系式，并求出S的最大值． -
科目： 来源： 题型：
查看答案和解析>>【题目】下列全国各地地铁标志图中，既是轴对称图形又是中心对称图形的是（ ）
A.
B.
C.
D.
-
科目： 来源： 题型：
查看答案和解析>>【题目】在某市开展的“体育、艺术2＋1”活动中，某校根据实际情况，决定主要开设A：乒乓球，B：篮球，C：跑步，D：跳绳这四种运动项目．为了解学生喜欢哪一种项目，随机抽取了部分学生进行调查，并将调查结果绘制成如图甲、乙所示的条形统计图和扇形统计图．请你结合图中的信息解答下列问题：
(1)求出所抽取的学生人数，并把条形统计图补充完整；
(2)样本中喜欢B项目的人数百分比是 ，其所在扇形统计图中的圆心角的度数是 ；
(3)已知该校有1 000人，根据样本估计全校喜欢跳绳的人数是多少？
图甲 图乙
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知不等式组
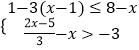的最小整数解为a，最大整数解为b，则ba=（ ）
A.
B.﹣8
C.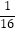
D.16 -
科目： 来源： 题型：
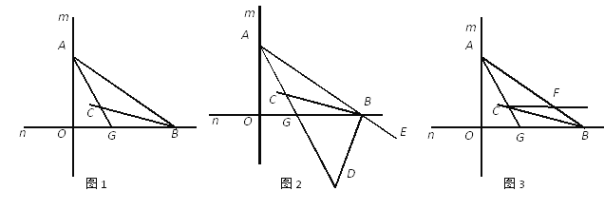
查看答案和解析>>【题目】如图1，直线m与直线n垂直相交于O，点A在直线m上运动，点B 在直线n上运动，AC、BC分别是∠BAO和∠ABO的角平分线．
（1）求∠ACB的大小；
（2）如图2，若BD是△AOB的外角∠OBE的角平分线，BD与AC相交于点D，点A、B在运动的过程中，∠ADB的大小是否会发生变化？若发生变化，请说明理由；若不发生变化，试求出其值；
（3）如图3，过C作直线与AB交于F，且满足∠AGO－∠BCF=45°，求证：CF∥OB．
相关试题
