【题目】在平面直角坐标系中,O为坐标原点.
(1)已知点A(3,1),连结OA,作如下探究:
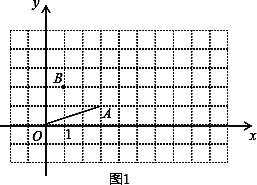
探究一:平移线段OA,使点O落在点B.设点A落在点C,若点B的坐标为(1,2),请在图1中作出BC,点C的坐标是_________;
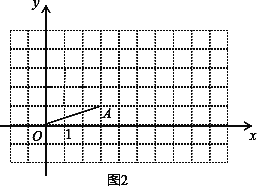
探究二:将线段OA绕点O逆时针旋转90°,设点A落在点D.则点D的坐标是_______.
(2) 已知四点O(0,0),A (a,b), C,B(c,d),顺次连结O,A,C,B.
若所得到的四边形是正方形,请直接写出a,b,c,d应满足的关系式是________.
参考答案:
【答案】 (4,3) (a+c,b+d); a=d且b=-c或b=c且a=-d.
【解析】(1)由于点A(3,1),连接OA,平移线段OA,使点O落在点B.设点A落在点C,若点B的坐标为(1,2),由此即可得到平移方法,然后利用平移方法即可确定在图1中作出BC,并且确定点C的坐标;又将线段OA绕点O逆时针旋转90度,设点A落在点D,根据旋转的性质和方向可以确定点D的坐标;
(2)已知四点O(0,0),A(a,b),C,B(c,d),顺次连接O,A,C,B.
①若所得到的四边形为平行四边形,那么得到OA∥CB,根据平移的性质和已知条件即可确定点C的坐标;
②若所得到的四边形是正方形,那么根据正方形的性质可以得到a=d且b=-c或b=c且a=-d.
解:(1)探究一:
∵点A(3,1),连接OA,平移线段OA,使点O落在点B.
设点A落在点C,若点B的坐标为(1,2),
则C的坐标为(4,3),如图1所示: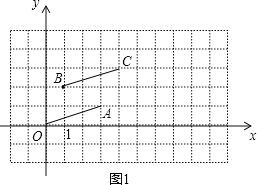
探究二:
∵将线段OA绕点O逆时针旋转90度,
设点A落在点D.
则点D的坐标是(-1,3),如图2所示;
(2)∵四点O(0,0),A(a,b),C,B(c,d),顺次连接O,A,C,B.
①若所得到的四边形为平行四边形,
那么OA∥CB,
∴OA平移到OB的位置,
点C的坐标为(a+c,b+d);
②若所得到的四边形是正方形,
那么根据正方形的性质可以得到a=d且b=-c或b=c且a=-d.
“点睛”此题分别考查了坐标与图形的变换、平由四边形、正方形的性质等知识,综合性比较强,要求学生熟练掌握相关的基础知识才能很好解决这类问题.
-
科目: 来源: 题型:
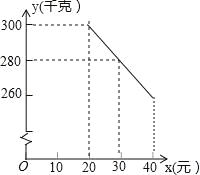
查看答案和解析>>【题目】(2016云南省第22题)草莓是云南多地盛产的一种水果,今年某水果销售店在草莓销售旺季,试销售成本为每千克20元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克40元,经试销发现,销售量y(千克)与销售单价x(元)符合一次函数关系,如图是y与x的函数关系图象.
(1)求y与x的函数解析式(也称关系式)
(2)设该水果销售店试销草莓获得的利润为W元,求W的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个直角三角形中,如果各边的长度都扩大5倍,那么它的两个锐角的余弦值________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016贵州省毕节市第27题)如图,已知抛物线
 与直线
与直线 交于A(a,8)、B两点,点P是抛物线上A、B之间的一个动点,过点P分别作
交于A(a,8)、B两点,点P是抛物线上A、B之间的一个动点,过点P分别作 轴、
轴、 轴的平行线与直线AB交于点C和点E.
轴的平行线与直线AB交于点C和点E.(1)求抛物线的解析式;
(2)若C 为AB中点,求PC的长;
(3)如图,以PC,PE为边构造矩形PCDE,设点D的坐标为(m,n),请求出m,n之间的关系式。

-
科目: 来源: 题型:
查看答案和解析>>【题目】用反证法证明,“在△ABC中,∠A、∠B对边是a、b,若∠A>∠B,则a>b.”第一步应假设_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】李飒的妈妈买了几瓶饮料,第一天,他们全家喝了全部饮料的一半零半瓶;第二天,李飒招待来家中玩的同学,又喝了第一天剩下的饮料的一半零半瓶;第三天,李飒索性将第二天所剩的饮料的一半零半瓶喝了.这三天,正好把妈妈买的全部饮料喝光,则妈妈买的饮料一共有多少瓶?
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式
(1)x3﹣6x2+9x;
(2)a2(x﹣y)+4(y﹣x).
相关试题

