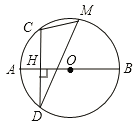
【题目】如图,线段AB 是⊙O的直径,弦CD⊥AB于点H,点M是弧CBD 上任意一点,AH=2,CH=4.
(1)求⊙O 的半径r 的长度;
(2)求sin∠CMD;
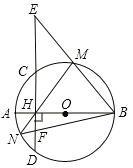
(3)直线BM交直线CD于点E,直线MH交⊙O 于点 N,连接BN交CE于点 F,求HE![]() HF的值.
HF的值.
参考答案:
【答案】(1)5;(2)![]() ;(3)16
;(3)16
【解析】(1)在Rt△COH中,利用勾股定理即可解决问题;
(2)只要证明∠CMD=△COA,求出sin∠COA即可;
(3)由△EHM∽△NHF,推出![]() ,推出HEHF=HMHN,又HMHN=AHHB,推出HEHF=AHHB,由此即可解决问题.
,推出HEHF=HMHN,又HMHN=AHHB,推出HEHF=AHHB,由此即可解决问题.
(1)连接OC,
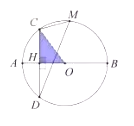
在Rt△COH中,
∵CH=4,OH=r-2,OC=r.
∴ (r-2)2+42=r2.
∴ r=5;
(2)∵弦CD与直径AB垂直,
∴![]() ,
,
∴ ∠AOC=![]() ∠COD,
∠COD,
∴∠CMD=![]() ∠COD,
∠COD,
∴ ∠CMD=∠AOC,
∴sin∠CMD=sin∠AOC,
在Rt△COH中,
∴sin∠AOC=![]() ,
,
∴sin∠CMD=![]() ;
;
(3)连接AM,
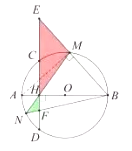
∴∠AMB=90°,
在Rt△AMB中,
∴∠MAB+∠ABM=90°,
在Rt△EHB中,
∴∠E+∠ABM=90°,
∴∠MAB=∠E,
∵![]() ,
,
∴∠MNB=∠MAB=∠E,
∵∠EHM=∠NHF,
∴△EHM∽△NHF,
∴![]() ,
,
∴HEHF=HMHN,
∵AB与MN交于点H,
∴HMHN=HAHB=HA(2r-HA)=2×(10-2)=16,
∴HEHF=16.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲同学在拼图探索活动中发现,用4个形状大小完全相同的直角三角形(直角边长分别为a,b,斜边长为c),可以拼成像如图1那样的正方形,并由此得出了关于a2,b2,c2的一个等式.
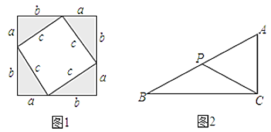
(1)请你写出这一结论:______,并给出验证过程.
(2)试用上述结论解决问题:如图2,P是Rt△ABC斜边AB上的一个动点,已知AC=5,AB=13,求PC的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB的函数解析式为y=-2x+8,与x轴交于点A,与y轴交于点B。
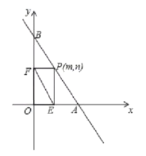
(1)求A、B两点的坐标;
(2)若点P(m,n)为线段AB上的一个动点(与A、B不重合),作PE⊥x轴于点E,PF⊥y轴于点F,连接E,若△PAO的面积为S,求S关于m的函数关系式,并写出m的取值范围。
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的一元二次方程ax2+bx﹣1=0(a≠0)有一根为x=2019,则一元二次方程a(x﹣1)2+b(x﹣1)=1必有一根为( )
A.
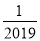 B.2020C.2019D.2018
B.2020C.2019D.2018 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠C=90°,AC=12,BC=9,AB=15,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒3个单位,设运动的时间为t秒.
(1)当t=______时,CP把△ABC的面积分成相等的两部分;
(2)当t=5时,CP把△ABC分成的两部分面积之比是S△APC:S△BPC=______
(3)当t=______时,△BPC的面积为18.

-
科目: 来源: 题型:
查看答案和解析>>【题目】探索规律:
观察下面由※组成的图案和算式,填空(直接写出答案):

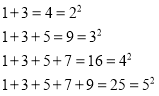
(1)请猜想1+3+5+7+9+11= ;
(2)请猜想1+3+5+7+9+……+(2n-1)= ;
(3)请用上述规律计算:41+43+45+……+97+99= .
相关试题

