【题目】探索规律:
观察下面由※组成的图案和算式,填空(直接写出答案):

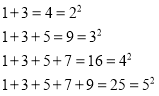
(1)请猜想1+3+5+7+9+11= ;
(2)请猜想1+3+5+7+9+……+(2n-1)= ;
(3)请用上述规律计算:41+43+45+……+97+99= .
参考答案:
【答案】(1)36;(2)n2;(3)2100.
【解析】
(1)根据已知得出从1开始的连续奇数之和等于数字个数的平方,进而得出答案;
(2)根据已知得出从1开始的连续奇数之和等于数字个数的平方,进而得出答案;
(3)根据题意得出原式=(1+3+5+…+97+99)-(1+3+5+…+37+39),进而求出即可.
(1)∵1+3=4=22
1+3+5=9=32
1+3+5+7=16=42
1+3+5+7+9=25=52
∴1+3+5+7+9+11=62=36.
故答案为:36;
(2)1+3+5+7+9+…+(2n-1)=n2.
故答案为:n2;
(3)41+43+45+…+97+99
=(1+3+5+…+97+99)-(1+3+5+…+37+39)
=502-202
=2500-400
=2100.
-
科目: 来源: 题型:
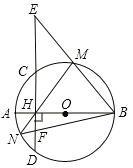
查看答案和解析>>【题目】如图,线段AB 是⊙O的直径,弦CD⊥AB于点H,点M是弧CBD 上任意一点,AH=2,CH=4.
(1)求⊙O 的半径r 的长度;
(2)求sin∠CMD;
(3)直线BM交直线CD于点E,直线MH交⊙O 于点 N,连接BN交CE于点 F,求HE
 HF的值.
HF的值.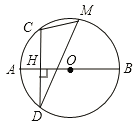
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠C=90°,AC=12,BC=9,AB=15,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒3个单位,设运动的时间为t秒.
(1)当t=______时,CP把△ABC的面积分成相等的两部分;
(2)当t=5时,CP把△ABC分成的两部分面积之比是S△APC:S△BPC=______
(3)当t=______时,△BPC的面积为18.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 ,
, ,点
,点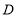 在边
在边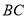 上(与
上(与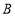 、
、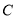 不重合),四边形
不重合),四边形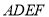 为正方形,过点
为正方形,过点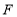 作
作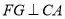 ,交
,交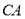 的延长线于点
的延长线于点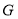 ,连接
,连接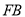 ,交
,交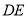 于点
于点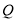 ,对于下列结论:①
,对于下列结论:①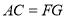 ;②四边形
;②四边形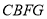 是矩形;③
是矩形;③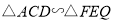 .其中正确的是( )
.其中正确的是( )
A.①②③B.①②C.①③D.②③
-
科目: 来源: 题型:
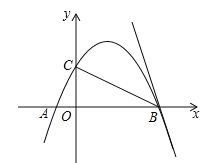
查看答案和解析>>【题目】(2017广东省深圳市)如图,抛物线
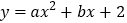 经过点A(﹣1,0),B(4,0),交y轴于点C;
经过点A(﹣1,0),B(4,0),交y轴于点C;(1)求抛物线的解析式(用一般式表示);
(2)点D为y轴右侧抛物线上一点,是否存在点D使
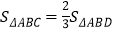 ?若存在请直接给出点D坐标;若不存在,请说明理由;
?若存在请直接给出点D坐标;若不存在,请说明理由;(3)将直线BC绕点B顺时针旋转45°,与抛物线交于另一点E,求BE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB为⊙O的直径,AB=2,AD和BE是圆O的两条切线,A、B为切点,过圆上一点C作⊙O的切线CF,分别交AD、BE于点M、N,连接AC、CB,若∠ABC=30°,则AM= .

相关试题

