【题目】已知,在△ABC中,AB=AC,点D、点O分别为BC、AC的中点,AE//BC.
(1)如图1,求证:四边形ADCE是矩形;
(2)如图2,若点 F是 CE上一动点,在不添加任何辅助线的情况下,请直接写出与四边形 ABDF 面积相等的三角形和四边形.

参考答案:
【答案】(1)证明见解析;(2)S△ABC,S四边形ABDE,S矩形ADCE
【解析】
(1)首先得到四边形ADCE是平行四边形,然后利用有一个角是直角的平行四边形是矩形判断矩形即可;
(2)根据四边形ADCE是矩形,得到AD∥CE,于是得到S△ADC=S△ADF=S△AED,即可得到结论.
(1)证明:∵点D、点O别是BC、AC的中点,
∴OD∥AB,
∴DE∥AB,
又∵AE∥BD,
∴四边形ABDE是平行四边形,
∵点D是BC的中点,
∴AE平行且等于DC,
∴四边形AECD是平行四边形,
∵AB=AC,D为BC的中点,
∴AD⊥BC,
∴四边形ADCE是矩形;
(2)解:∵四边形ADCE是矩形,
∴AD∥CE,
∴S△ADC=S△ADF=S△AED,
∴四边形ABDF面积=S△ABC=S四边形ABDE=S矩形ADCE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一家商铺进行维修,若请甲、乙两名工人同时施工,
 天可以完成,共需支付两人工资
天可以完成,共需支付两人工资 元,若先请甲工人单独做
元,若先请甲工人单独做 天,再请乙工人单独做
天,再请乙工人单独做 天也可完成,共需付给两人工资
天也可完成,共需付给两人工资 元
元 甲、乙工人单独工作一天,商铺应分别支付多少工资?
甲、乙工人单独工作一天,商铺应分别支付多少工资? 单独请哪名工人完成,商铺支付维修费用较少?
单独请哪名工人完成,商铺支付维修费用较少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC=90°,D为AB边上一点(BD<BC),AE⊥AB,AE=BD,连接DE交AC于F,若∠AFE=45°,AD=3
 ,CD=5,则线段AC的长度为_________.
,CD=5,则线段AC的长度为_________.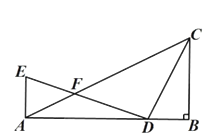
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线l1:y=kx+b与直线l2:y=bx+k在同一坐标系中的大致位置是( )
A.
 B.
B. 
C.
 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是我市某一天内的气温变化图,根据图象,下列说法中错误的是( )

A.这一天中最高气温是26℃
B.这一天中最高气温与最低气温的差为16℃
C.这一天中2时至14时之间的气温在逐渐升高
D.这一天中14时至24时之间的气温在逐渐降低
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A,B在反比例函数y=
 (x>0)的图象上,点C,D在反比例函数y=
(x>0)的图象上,点C,D在反比例函数y= (k>0)的图象上,AC∥BD∥y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为
(k>0)的图象上,AC∥BD∥y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为 ,则k的值为_____.
,则k的值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,观察由棱长为
 的小立方体摆成的图形,寻找规律:如图 ① 中,共有
的小立方体摆成的图形,寻找规律:如图 ① 中,共有  个小立方体,其中
个小立方体,其中  个看得见,
个看得见,  个看不见;如图 ② 中,共有
个看不见;如图 ② 中,共有  个小立方体,其中
个小立方体,其中  个看得见,
个看得见,  个看不见;如图 ③ 中,共有
个看不见;如图 ③ 中,共有  个小立方体,其中
个小立方体,其中  个看得见,
个看得见,  个看不见;
个看不见;  ,则第 ⑥个图中,看得见的小立方体有________________个.
,则第 ⑥个图中,看得见的小立方体有________________个.
相关试题

