Question

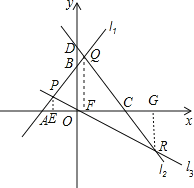
【题目】如图，已知直线l1：y=x+3与x轴交于点A，与y轴交于点B，与直线l2：y=﹣x交于点P．直线l3：y=﹣x+4与x轴交于点C，与y轴交于点D，与直线l1交于点Q，与直线l2交于点R．

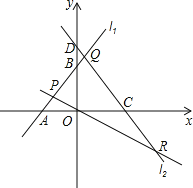
（1）点A的坐标是 ，点B的坐标是 ，点P的坐标是 ；

（2）将△POB沿y轴折叠后，点P的对应点为P′，试判断点P′是否在直线l3上，并说明理由；

（3）求△PQR的面积．

Answer 1

【答案】（1）（﹣3，0），（0，3），（﹣2，1）；（2）见解析；（3）．

【解析】

试题分析：（1）直线l1：y=x+3与x轴交于点A，与y轴交于点B，令y=0，求得x=﹣3，令x=0，求得y=3，得到A、B的坐标将直线l1：y=x+3和直线l2：y=﹣x联立组成有关x、y的方程组，解方程就能求出两直线的交点P坐标；

（2）求得P′的坐标，代入y=﹣x+4即可判断；

（3）求得Q、R、C点的坐标，然后根据即可求得．

解：（1）∵直线l1：y=x+3与x轴交于点A，与y轴交于点B，

∴令y=0，求得x=﹣3，令x=0，求得y=3，

∴A（﹣3，0）、B（0，3），

∵直线l1与直线l2y=﹣x交于点P．

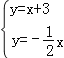∴解得，

∴P（﹣2，1），

故答案为：（﹣3，0），（0，3），（﹣2，1）；

（2）点P在直线l3上

∵P（﹣2，1），且将△POB沿y轴折叠后，点P与点P关于y轴对称，

∴P（2，1），

当x=2时，代入y=﹣x+4得y=﹣×2+4=1，

∴点P在直线l3上；

（3）分别过点P作PE⊥x轴于F，过点Q作QF⊥x轴于F，过点R作RG⊥x轴于G，

由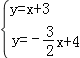 得，

∴Q（，），

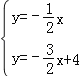由 得

∴R（4，﹣2），

对于y=﹣x+4，则y=0得x=，

∴C（，0），

∴S△AQC=AC×QF=×（+3）×=，S△OCR=OCGR=××2=，S△AOP=OAPE=×3×1=，

∴S△PQR=S△AQC+S△OCR﹣S△AOP=+﹣=．