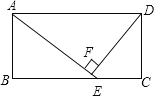
【题目】如图,矩形ABCD中,E为BC上一点,DF⊥AE于F.

(1)△ABE与△ADF相似吗?请说明理由.
(2)若AB=6,AD=12,BE=8,求DF的长.
参考答案:
【答案】(1)△ABE∽△DFA.(2)7.2.
【解析】
试题分析:(1)根据矩形的性质和DF⊥AE,可得∠ABE=∠AFD=90°,∠AEB=∠DAF,即可证明△ABE∽△DFA.
(2)利用△ABE∽△ADF,得![]() =
=![]() ,再利用勾股定理,求出AE的长,然后将已知数值代入即可求出DF的长.
,再利用勾股定理,求出AE的长,然后将已知数值代入即可求出DF的长.
解:(1)△ABE与△ADF相似.理由如下:
∵四边形ABCD为矩形,DF⊥AE,
∴∠ABE=∠AFD=90°,
∠AEB=∠DAF,
∴△ABE∽△DFA.
(2)∵△ABE∽△ADF
∴![]() =
=![]() ,
,
∵在Rt△ABE中,AB=6,BE=8,
∴AE=10
∴DF=![]() =
=![]() =7.2.
=7.2.
答:DF的长为7.2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小亮房间窗户的窗帘如图1所示,它是由两个四分之一圆组成(半径相同)
(1)用代数式表示窗户能射进阳光的面积是 .(结果保留π)
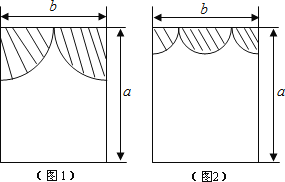
(2)当
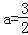 ,b=1时,求窗户能射进阳光的面积是多少?(取π≈3)
,b=1时,求窗户能射进阳光的面积是多少?(取π≈3)(3)小亮又设计了如图2的窗帘(由一个半圆和两个四分之一圆组成,半径相同),请你帮他算一算此时窗户能射进阳光的面积是否更大?如果更大,那么大多少?(结果保留π)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某食品公司产销一种食品,已知每月的生产成本y1与产量x之间是一次函数关系,函数y1与自变量z(kg)的部分对应值如下表:
x(单位:kg)
10
20
30
y1(单位:/元)
3030
3060
3090
(1)求y1与x之间的函数关系式;
(2)经过试销发现,这种食品每月的销售收入y2(元)与销量x(kg)之间满足如图所示的函数关系
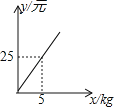
①y2与x之间的函数关系式为 ;
②假设该公司每月生产的该种食品均能全部售出,那么该公司每月至少要生产该种食品多少kg,才不会亏损?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,AC、DC为弦,∠ACD=60°,P为AB延长线上的点,∠APD=30°.
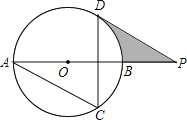
(1)求证:DP是⊙O的切线;
(2)若⊙O的半径为3cm,求图中阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a2﹣a﹣1=0,则a3﹣a2﹣a+2016=__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:26=a2=4b,则a+b= ______ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线l1:y=x+3与x轴交于点A,与y轴交于点B,与直线l2:y=﹣
 x交于点P.直线l3:y=﹣
x交于点P.直线l3:y=﹣ x+4与x轴交于点C,与y轴交于点D,与直线l1交于点Q,与直线l2交于点R.
x+4与x轴交于点C,与y轴交于点D,与直线l1交于点Q,与直线l2交于点R.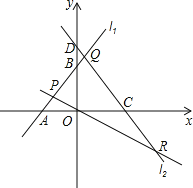
(1)点A的坐标是 ,点B的坐标是 ,点P的坐标是 ;
(2)将△POB沿y轴折叠后,点P的对应点为P′,试判断点P′是否在直线l3上,并说明理由;
(3)求△PQR的面积.
相关试题

