【题目】如图,△ABC中,AC=BC,点D在BC上,作∠ADF=∠B,DF交外角∠ACE的平分线CF于点F.

(1)求证:CF∥AB;
(2)若∠CAD=20°,求∠CFD的度数.
参考答案:
【答案】(1)见解析;(2)20°
【解析】
试题分析:(1)根据三角形的性质得到∠B=∠BAC,由三角形外角的性质得到∠ACE=∠B+∠BAC,求得∠BAC=![]() ,由角平分线的定义得到∠ACF=∠ECF=
,由角平分线的定义得到∠ACF=∠ECF=![]() ,等量代换得到∠BAC=∠ACF,根据平行线的判定定理即可得到结论;
,等量代换得到∠BAC=∠ACF,根据平行线的判定定理即可得到结论;
(2)由等量代换得到∠ACF=∠ADF,根据三角形的内角和得到∠ADF+∠CAD+∠AGD=180°,∠ACF+∠F+∠CGF=180°,由于∠AGD=∠CGF,即可得到结论.
(1)证明:∵AC=BC,
∴∠B=∠BAC,
∵∠ACE=∠B+∠BAC,
∴∠BAC=![]() ,
,
∵CF平分∠ACE,
∴∠ACF=∠ECF=![]() ,
,
∴∠BAC=∠ACF,
∴CF∥AB;
(2)解:∵∠BAC=∠ACF,∠B=∠BAC,∠ADF=∠B,
∴∠ACF=∠ADF,
∵∠ADF+∠CAD+∠AGD=180°,∠ACF+∠F+∠CGF=180°,
又∵∠AGD=∠CGF,
∴∠F=∠CAD=20°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a2﹣a﹣1=0,则a3﹣a2﹣a+2016=__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:26=a2=4b,则a+b= ______ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线l1:y=x+3与x轴交于点A,与y轴交于点B,与直线l2:y=﹣
 x交于点P.直线l3:y=﹣
x交于点P.直线l3:y=﹣ x+4与x轴交于点C,与y轴交于点D,与直线l1交于点Q,与直线l2交于点R.
x+4与x轴交于点C,与y轴交于点D,与直线l1交于点Q,与直线l2交于点R.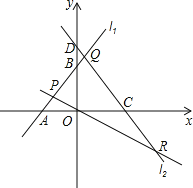
(1)点A的坐标是 ,点B的坐标是 ,点P的坐标是 ;
(2)将△POB沿y轴折叠后,点P的对应点为P′,试判断点P′是否在直线l3上,并说明理由;
(3)求△PQR的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某旅游景点的门票价格如下表:
购票人数/人
1﹣50
51﹣100
100以上
每人门票价/元
80
75
70
某校八年级(1)、(2)两班共100多人计划去游览该景点,其中(1)班人数少于50人,(2)班人数有50多人,如果两班都以班为单位单独购票,则一共支付7965元;如果两班联合起来作为一个团体购票,则只需花费7210元.两个班各有多少名学生?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=-2x+4的图象与y轴的交点坐标是( )
A.(0,4) B.(4,0) C.(2,0) D.(0,2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为4cm,动点P、Q同时从点A出发,以1cm/s的速度分别沿A→B→C和A→D→C的路径向点C运动,设运动时间为x(单位:s),四边形PBDQ的面积为y(单位:cm2),则y与x(0≤x≤8)之间的函数关系可用图象表示为 ( )
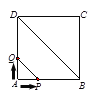
A.
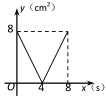 B.
B. 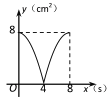 C.
C. 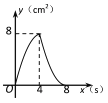 D.
D. 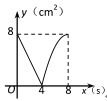
相关试题

