【题目】已知反比例函数![]() 的图象如图2,则一元二次
的图象如图2,则一元二次
方程![]() 根的情况是( )
根的情况是( )
A.有两个不等实根B.有两个相等实根
C.没有实根 D.无法确定。
参考答案:
【答案】C
【解析】首先根据反比例函数![]()
的图象可以得到k的取值范围,然后根据k的取值范围即可判断方程x2-(2k-1)x+k2-1=0的判别式的正负情况,接着就可以判断方程的根的情况.
解:∵反比例函数![]()
的图象在第一、三象限内,
∴k-2>0,
∴k>2,
∵一元二次方程x2-(2k-1)x+k2-1=0的判别式为
△=b2-4ac=(2k-1)2-4(k2-1)=-4k+5,
而k>2,
∴-4k+5<0,
∴△<0,
∴一元二次方程x2-(2k-1)x+k2-1=0没有实数根.
故选C.
此题考查了反比例函数的图象和性质及一元二次方程判别式的应用,一元二次方程根的情况与判别式△的关系:
(1)△>0方程有两个不相等的实数根;
(2)△=0方程有两个相等的实数根;
(3)△<0方程没有实数根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】星期天,玲玲骑自行车到郊外游玩,她离家的距离与时间的关系如图所示,请根据图象回答下列问题.
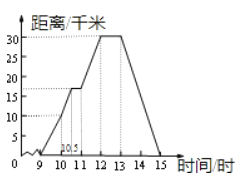
(1)玲玲到达离家最远的地方是什么时间?离家多远?
(2)她何时开始第一次休息?休息了多长时间?
(3)她骑车速度最快是在什么时候?车速多少?
(4)玲玲全程骑车的平均速度是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】(3x2y﹣2x+1)(﹣2xy)
-
科目: 来源: 题型:
查看答案和解析>>【题目】若△ABC∽△ABC,∠A=40°,∠B=110°,则∠C=( ).
A.40°
B.110°
C.70°
D.30° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AB=8,BC=12,分别以AB、AC为直径作半圆,则图中阴影部分的面积是为________________.
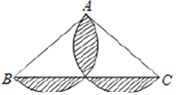
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AB=3,BC=5,以点B的圆心,以任意长为半径作弧,分别交BA、BC于点P、Q,再分别以P、Q为圆心,以大于
 PQ的长为半径作弧,两弧在∠ABC内交于点M,连接BM并延长交AD于点E,则DE的长为_____.
PQ的长为半径作弧,两弧在∠ABC内交于点M,连接BM并延长交AD于点E,则DE的长为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,DE垂直平分AC , DF⊥BC , 当△ABC满足条件时,四边形DECF是正方形.(要求:①不再添加任何辅助线,②只需填一个符合要求的条件)

相关试题

