【题目】星期天,玲玲骑自行车到郊外游玩,她离家的距离与时间的关系如图所示,请根据图象回答下列问题.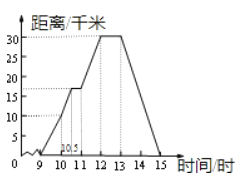
(1)玲玲到达离家最远的地方是什么时间?离家多远?
(2)她何时开始第一次休息?休息了多长时间?
(3)她骑车速度最快是在什么时候?车速多少?
(4)玲玲全程骑车的平均速度是多少?
参考答案:
【答案】
(1)
解答:观察图象可知:玲玲到离家最远的地方需要12小时,此时离家30千米;
(2)
开始第一次休息是10.5时,休息了0.5小时。
(3)
9~10时,速度为10÷(10-9)=10千米/时;
10~10.5时,速度约为(17.5-10)÷(10.5-10)=15千米/小时;
10.5~11时,速度为0;
11~12时,速度为(30-17.5)÷(12-11)=12.5千米/小时;
12~13时,速度为0;
13~15时,在返回的途中,速度为:30÷(15-13)=15千米/小时;
可见骑行最快有两段时间:10~10.5时;13~15时.两段时间的速度都是15千米/小时.
(4)
解答:玲玲全程骑车的平均速度为:(30+30)÷(15-9)=10(千米/小时)
答:玲玲全程骑车的平均速度是10千米/小时.
【解析】 (1)利用图中的点的横坐标表示时间,纵坐标表示离家的距离,进而得出答案;(2)休息是路程不在随时间的增加而增加;(3)往返全程中求算最快速度,用距离除以所用时间即可;(4)用玲玲全称所行的路程除以所用的时间即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CE=2DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③EG=DE+BG;④AG∥CF;⑤S△FGC=3.6.其中正确结论的个数是( )
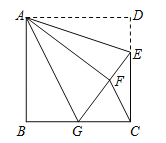
A.2 B.3 C.4 D.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边三角形ABC的边长为2,过点B的直线
 ⊥AB,且△ABC与△A′BC′关于直线
⊥AB,且△ABC与△A′BC′关于直线 对称,D为线段BC′上一动点,则AD + CD的最小值是( )
对称,D为线段BC′上一动点,则AD + CD的最小值是( )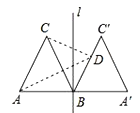
A. 4 B.
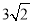 C.
C. 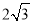 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个多项式与2x2﹣3x﹣1的和等于x2﹣2x﹣3,则这个多项式是( )
A.﹣x2+2x+2
B.﹣x2+x+2
C.x2﹣x+2
D.﹣x2+x﹣2 -
科目: 来源: 题型:
查看答案和解析>>【题目】(3x2y﹣2x+1)(﹣2xy)
-
科目: 来源: 题型:
查看答案和解析>>【题目】若△ABC∽△ABC,∠A=40°,∠B=110°,则∠C=( ).
A.40°
B.110°
C.70°
D.30° -
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数
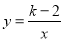 的图象如图2,则一元二次
的图象如图2,则一元二次方程
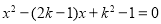 根的情况是( )
根的情况是( )A.有两个不等实根B.有两个相等实根
C.没有实根 D.无法确定。
相关试题

