【题目】如图,已知抛物线y=ax2+bx+c(a<0)的对称轴为x=1,交x轴的一个交点为(x1 , 0),且﹣1<x1<0,有下列5个结论:①abc>0;②9a﹣3b+c<0;③2c<3b;④(a+c)2<b2;⑤a+b>m(am+b)(m≠1的实数)其中正确的结论有( )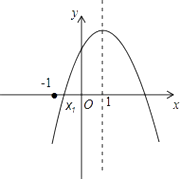
A.1个
B.2个
C.3个
D.4个
参考答案:
【答案】D
【解析】①抛物线对称轴在y轴的右侧,则a、b异号,即b>0.
抛物线与y轴交于正半轴,则c>0.
∵a<0,
∴abc<0.
故①错误;②由图示知,当x=3时,y<0,即9a3b+c<0,故②正确;③由图示知,x=1时,y<0,即ab+c<0,
∵x= ![]() =1,
=1,
∴a= ![]() b,
b,
∴ab+c= ![]() bb+c<0,即2c<3b,故③正确;④由图示知,x=1时,y>0,即a+b+c>0
bb+c<0,即2c<3b,故③正确;④由图示知,x=1时,y>0,即a+b+c>0
∵ab+c<0,
∴(a+b+c)(ab+c)<0,则(a+c)2b2<0,
∴(a+c)2<b2;
故④正确;⑤∵当x=1时,y最大,即a+b+c最大,故a+b+c>am2+bm+c,即a+b>m(am+b),(m为实数且m≠1),故⑤正确。
综上所述,其中正确的结论有4个。
所以答案是:D.
【考点精析】通过灵活运用二次函数的性质和二次函数图象以及系数a、b、c的关系,掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小;二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c)即可以解答此题.
-
科目: 来源: 题型:
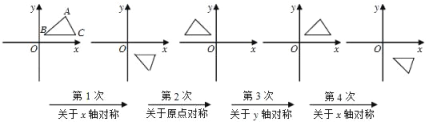
查看答案和解析>>【题目】如图,在平面直角坐标系中,对△ABC进行循环反复的轴对称或中心对称变换,若原来点A的坐标是(a,b),则经过第2018次变换后所得的A点坐标是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解答下列应用题:
⑴某房间的面积为17.6m2,房间地面恰好由110块相同的正方形地砖铺成,每块地砖的边长是多少?
⑵已知第一个正方体水箱的棱长是60cm,第二个正方体水箱的体积比第一个水箱的体积的3倍还多81000 cm3,则第二个水箱需要铁皮多少平方米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)在下面的括号内,填上推理的依据.
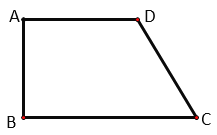
①如图1,
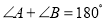 ,求证
,求证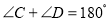
证明:
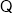
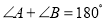 ,
,
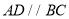 (_____________)
(_____________)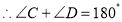 (_____________)
(_____________)
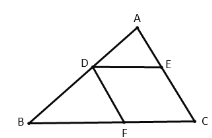
②如图2,
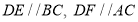 ,求证
,求证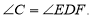
证明:
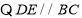 ,
,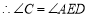 (_____________)
(_____________)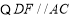
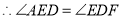 (_____________)
(_____________)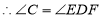 (_____________)
(_____________)
(2)如图,直线
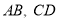 相交于点
相交于点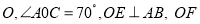 平分
平分 求①
求①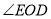 的度数;②
的度数;② 的度数.
的度数.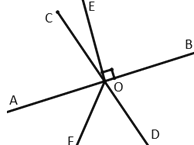
-
科目: 来源: 题型:
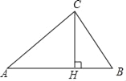
查看答案和解析>>【题目】如图,学校有一块三角形草坪,数学课外小组的同学测得其三边的长分别为AB=200米,AC=160米,BC=120米.
(1)小明根据测量的数据,猜想△ABC是直角三角形,请判断他的猜想是否正确,并说明理由;
(2)若计划修一条从点C到BA边的小路CH,使CH⊥AB于点H,求小路CH的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)根据下表回答:

1
1.7
1.73
1.74
1.8
2
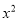
1
2.89
2.9929
3.0276
3.24
4
①
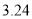 的平方根是_____________;
的平方根是_____________;②由表可知,
 在表中哪两个相邻的数之间(小数部分是两位小数)?
在表中哪两个相邻的数之间(小数部分是两位小数)?(2)如图,在平面直角坐标系中,已知三点



①三角形
 的面积是_______
的面积是_______②分别将
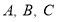 三点的横坐标乘
三点的横坐标乘 ,纵坐标加
,纵坐标加 ,记坐标变换后
,记坐标变换后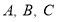 所对的点分别为
所对的点分别为 在坐标系中画出以这三点为顶点的三角形
在坐标系中画出以这三点为顶点的三角形
-
科目: 来源: 题型:
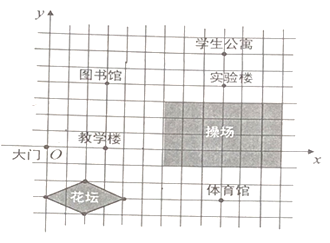
查看答案和解析>>【题目】(1)如图,是某学校的平面简图,以学校大门位置为坐标原点建立平面直角坐标系.写出图中教学楼、图书馆、体育馆、实验楼、学生公寓位置的坐标(网格小正方形的边长记为1个长度单位).
教学楼:_____________;
图书馆:_____________;
体育馆:_____________;
实验楼:_____________;
学生公寓:_____________;
(2)点
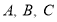 在坐标系中的位置如图所示,三角形
在坐标系中的位置如图所示,三角形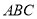 的面积为
的面积为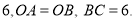
①三角形
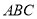 三个顶点的坐标分别为:
三个顶点的坐标分别为: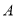 (____,____),
(____,____),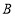 (____,_____),
(____,_____),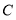 (__,__);
(__,__);②点
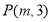 是一动点,若三角形
是一动点,若三角形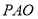 面积等于三角形
面积等于三角形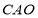 面积.求点
面积.求点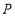 坐标.
坐标.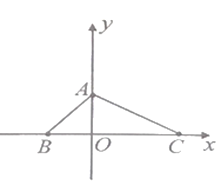
相关试题

