【题目】如图,在Rt△ABC中,∠ACB=90°,AC=5cm,∠BAC=60°,动点M从点B出发,在BA边上以每秒2cm的速度向点A匀速运动,同时动点N从点C出发,在CB边上以每秒 ![]() cm的速度向点B匀速运动,设运动时间为t秒(0≤t≤5),连接MN.
cm的速度向点B匀速运动,设运动时间为t秒(0≤t≤5),连接MN.
(1)若BM=BN,求t的值;
(2)若△MBN与△ABC相似,求t的值;
(3)当t为何值时,四边形ACNM的面积最小?并求出最小值.
参考答案:
【答案】
(1)
解:∵在Rt△ABC中,∠ACB=90°,AC=5,∠BAC=60°,
∴∠B=30°,
∴AB=2AC=10,BC=5 ![]() .
.
由题意知:BM=2t,CN= ![]() t,
t,
∴BN=5 ![]() -
- ![]() t,
t,
∵BM=BN,
∴2t=5 ![]() -
- ![]() t
t
解得: ![]() .
.
(2)
解:分两种情况:①当△MBN∽△ABC时,
则 ![]() ,即
,即 ![]() ,
,
解得:t= ![]() .
.
②当△NBM∽△ABC时,
则 ![]() ,即
,即 ![]() ,
,
解得:t= ![]() .
.
综上所述:当t= ![]() 或t=
或t= ![]() 时,△MBN与△ABC相似.
时,△MBN与△ABC相似.
(3)
解:过M作MD⊥BC于点D,则MD∥AC,
∴△BMD∽△BAC,
∴ ![]() ,
,
即 ![]() ,
,
解得:MD=t.
设四边形ACNM的面积为y,
∴y= ![]() =
= ![]() =
= ![]() .
.
∴根据二次函数的性质可知,当t= ![]() 时,y的值最小.
时,y的值最小.
此时, ![]() .
.
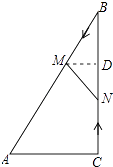
【解析】(1)由已知条件得出AB=10,BC=5 ![]() . 由题意知:BM=2t,CN=
. 由题意知:BM=2t,CN= ![]() t,BN=5
t,BN=5 ![]() -
- ![]() t,由BM=BN得出方程2t=5
t,由BM=BN得出方程2t=5 ![]() -
- ![]() t,解方程即可;(2)分两种情况:①当△MBN∽△ABC时,由相似三角形的对应边成比例得出比例式,即可得出t的值;②当△NBM∽△ABC时,由相似三角形的对应边成比例得出比例式,即可得出t的值;(3)过M作MD⊥BC于点D,则MD∥AC,证出△BMD∽△BAC,得出比例式求出MD=t.四边形ACNM的面积y=△ABC的面积﹣△BMN的面积,得出y是t的二次函数,由二次函数的性质即可得出结果.
t,解方程即可;(2)分两种情况:①当△MBN∽△ABC时,由相似三角形的对应边成比例得出比例式,即可得出t的值;②当△NBM∽△ABC时,由相似三角形的对应边成比例得出比例式,即可得出t的值;(3)过M作MD⊥BC于点D,则MD∥AC,证出△BMD∽△BAC,得出比例式求出MD=t.四边形ACNM的面积y=△ABC的面积﹣△BMN的面积,得出y是t的二次函数,由二次函数的性质即可得出结果.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正方形ABCD的边长为1,点P为正方形内一动点,若点M在AB上,且满足△PBC∽△PAM,延长BP交AD于点N,连结CM.

(1)如图一,若点M在线段AB上,求证:AP⊥BN;AM=AN;
(2)①如图二,在点P运动过程中,满足△PBC∽△PAM的点M在AB的延长线上时,AP⊥BN和AM=AN是否成立?(不需说明理由)
②是否存在满足条件的点P,使得PC= ?请说明理由.
?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,抛物线y=ax2﹣6x+c与x轴交于点A(﹣5,0)、B(﹣1,0),与y轴交于点C(0,﹣5),点P是抛物线上的动点,连接PA、PC,PC与x轴交于点D.
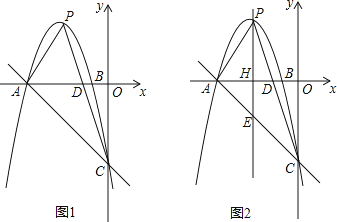
(1)求该抛物线所对应的函数解析式;
(2)若点P的坐标为(﹣2,3),请求出此时△APC的面积;
(3)过点P作y轴的平行线交x轴于点H,交直线AC于点E,如图2.
①若∠APE=∠CPE,求证: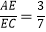 ;
;
②△APE能否为等腰三角形?若能,请求出此时点P的坐标;若不能,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,长方形的两边长分别为m+3,m+13;如图2的长方形的两边长分别为m+5,m+7.(其中m为正整数)

(1)写出两个长方形的面积S1,S2,并比较S1,S2的大小;
(2)现有一个正方形的周长与图1中的长方形的周长相等.试探究该正方形的面积与长方形的面积的差是否是一个常数,如果是,求出这个常数;如果不是,说明理由.
(3)在(1)的条件下,若某个图形的面积介于S1,S2之间(不包括S1,S2)且面积为整数,这样的整数值有且只有19个,求m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等边三角形,AE=CD,AD、BE相交于点P,BQ⊥DA于Q.
(1)求∠BPQ的度数;
(2)若PQ=3,EP=1,求AD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,二次函数y=﹣x2+bx+c的图象过点A(3,0),B(0,4)两点,动点P从A出发,在线段AB上沿A→B的方向以每秒2个单位长度的速度运动,过点P作PD⊥y于点D,交抛物线于点C.设运动时间为t(秒).
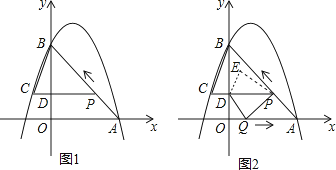
(1)求二次函数y=﹣x2+bx+c的表达式;
(2)连接BC,当t= 时,求△BCP的面积;
时,求△BCP的面积;
(3)如图2,动点P从A出发时,动点Q同时从O出发,在线段OA上沿O→A的方向以1个单位长度的速度运动.当点P与B重合时,P、Q两点同时停止运动,连接DQ,PQ,将△DPQ沿直线PC折叠得到△DPE.在运动过程中,设△DPE和△OAB重合部分的面积为S,直接写出S与t的函数关系及t的取值范围.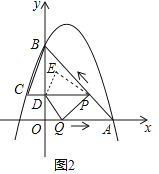
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2﹣2ax+c(a<0)的最大值为4,且抛物线过点(
 ,﹣
,﹣  ),点P(t,0)是x轴上的动点,抛物线与y轴交点为C,顶点为D.
),点P(t,0)是x轴上的动点,抛物线与y轴交点为C,顶点为D.
(1)求该二次函数的解析式,及顶点D的坐标;
(2)求|PC﹣PD|的最大值及对应的点P的坐标;
(3)设Q(0,2t)是y轴上的动点,若线段PQ与函数y=a|x|2﹣2a|x|+c的图象只有一个公共点,求t的取值.
相关试题

