搜索
【题目】如图，△ABC是等边三角形，AE=CD，AD、BE相交于点P，BQ⊥DA于Q．
（1）求∠BPQ的度数；
（2）若PQ=3，EP=1，求AD的长．
参考答案：
【答案】（1）60°；（2）7.
【解析】
（1）根据SAS证明△ABE≌△CAD，然后根据全等三角形的性质得出∠ABE=∠CAD，进而解答即可；
（2）根据含30°的直角三角形的性质解答即可．
解：（1）∵△ABC为等边三角形，
∴AB=AC，∠BAC=∠C=60°，
在△ABE与△CAD中，
，
∴△ABE≌△CAD（SAS）
∴∠ABE=∠CAD，AD=BE，
∴∠BPQ=∠BAD+∠ABE=∠BAD+∠CAD=60°；
（2）∵BQ⊥AD，∠BPQ=60°，
∴∠PBQ=30°，
∴BP=2PQ=6，
又∵AD=BE，
∴BE=BP+PE=6+1=7．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，抛物线y=ax2﹣6x+c与x轴交于点A（﹣5，0）、B（﹣1，0），与y轴交于点C（0，﹣5），点P是抛物线上的动点，连接PA、PC，PC与x轴交于点D．
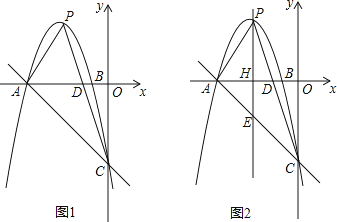
（1）求该抛物线所对应的函数解析式；
（2）若点P的坐标为（﹣2，3），请求出此时△APC的面积；
（3）过点P作y轴的平行线交x轴于点H，交直线AC于点E，如图2．
①若∠APE=∠CPE，求证：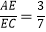
；
②△APE能否为等腰三角形？若能，请求出此时点P的坐标；若不能，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，长方形的两边长分别为m+3，m+13；如图2的长方形的两边长分别为m+5，m+7．（其中m为正整数）
（1）写出两个长方形的面积S1，S2，并比较S1，S2的大小；
（2）现有一个正方形的周长与图1中的长方形的周长相等．试探究该正方形的面积与长方形的面积的差是否是一个常数，如果是，求出这个常数；如果不是，说明理由．
（3）在（1）的条件下，若某个图形的面积介于S1，S2之间（不包括S1，S2）且面积为整数，这样的整数值有且只有19个，求m的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在Rt△ABC中，∠ACB=90°，AC=5cm，∠BAC=60°，动点M从点B出发，在BA边上以每秒2cm的速度向点A匀速运动，同时动点N从点C出发，在CB边上以每秒
cm的速度向点B匀速运动，设运动时间为t秒（0≤t≤5），连接MN．
（1）若BM=BN，求t的值；
（2）若△MBN与△ABC相似，求t的值；
（3）当t为何值时，四边形ACNM的面积最小？并求出最小值． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，二次函数y=﹣x2+bx+c的图象过点A（3，0），B（0，4）两点，动点P从A出发，在线段AB上沿A→B的方向以每秒2个单位长度的速度运动，过点P作PD⊥y于点D，交抛物线于点C．设运动时间为t（秒）．
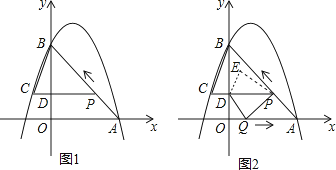
（1）求二次函数y=﹣x2+bx+c的表达式；
（2）连接BC，当t=
时，求△BCP的面积；
（3）如图2，动点P从A出发时，动点Q同时从O出发，在线段OA上沿O→A的方向以1个单位长度的速度运动．当点P与B重合时，P、Q两点同时停止运动，连接DQ，PQ，将△DPQ沿直线PC折叠得到△DPE．在运动过程中，设△DPE和△OAB重合部分的面积为S，直接写出S与t的函数关系及t的取值范围．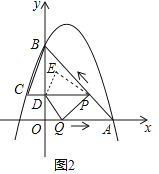
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知二次函数y=ax2﹣2ax+c（a＜0）的最大值为4，且抛物线过点（
，﹣ 
），点P（t，0）是x轴上的动点，抛物线与y轴交点为C，顶点为D．
（1）求该二次函数的解析式，及顶点D的坐标；
（2）求|PC﹣PD|的最大值及对应的点P的坐标；
（3）设Q（0，2t）是y轴上的动点，若线段PQ与函数y=a|x|2﹣2a|x|+c的图象只有一个公共点，求t的取值． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC中，∠BAC=120°，AB=AC=6．P是底边BC上的一个动点（P与B、C不重合），以P为圆心，PB为半径的⊙P与射线BA交于点D，射线PD交射线CA于点E．
（1）若点E在线段CA的延长线上，设BP=x，AE=y，求y关于x的函数关系式，并写出x的取值范围．
（2）当BP=2
时，试说明射线CA与⊙P是否相切．
（3）连接PA，若S△APE=
S△ABC ， 求BP的长．
相关试题
