【题目】如图,O是直线AB上一点,OC为任一条射线,OM平分∠AOC,ON平分∠BOC.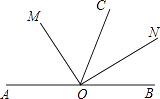
(1)图中与∠AON互补的角有;
(2)猜想∠MON的度数为 , 试说明理由.
参考答案:
【答案】
(1)∠CON、∠BON
(2)解:∠MON=90°,∵ON平分∠BOC,OM平分∠AOC,∴∠CON= ![]() ∠BOC,∠COM=
∠BOC,∠COM= ![]() ∠COA,∴∠MON=
∠COA,∴∠MON= ![]() ∠BOC+
∠BOC+ ![]() ∠COA=90°
∠COA=90°
【解析】解:(1)∵ON平分∠BOC,
∴∠CON=∠BON,
∵∠BON+∠AON=180°,
∴∠CON+∠AON=180°,
∴与∠AON互补的角有∠CON、∠BON,
故答案为:∠CON、∠BON;
(1)当两角之和为180°,则这两个角互补。根据图形可知∠BON和∠AON互补,根据角平分线的定义(ON平分∠BOC),得出∠CON=∠BON,即可得出与∠AON互补的角。
(2)根据角平分线的定义,分别得出∠CON与 ∠BOC,∠COM与 ∠COA的数量关系,再根据∠MON=∠CON+∠COM,即可得出结论。
-
科目: 来源: 题型:
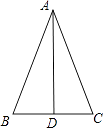
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AD平分∠BAC. 求证:△ABD≌△ACD.
-
科目: 来源: 题型:
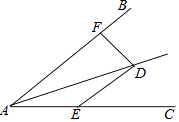
查看答案和解析>>【题目】如图:∠DAE=∠ADE=15°,DE∥AB,DF⊥AB,若AE=10,则DF等于 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数y=
 的图象如图所示,则一元二次方程x2-(2k-1)x+k2-1=0根的情况是( )
的图象如图所示,则一元二次方程x2-(2k-1)x+k2-1=0根的情况是( )
A. 没有实根 B. 有两个不等实根 C. 有两个相等实根 D. 无法确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b,c,是△ABC的三边,且满足a2b﹣a2c=b3﹣b2c,则△ABC的形状为( )
A. 等腰三角形 B. 直角三角形 C. 等边三角形 D. 任意三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△AOB中,OA=OB=8,∠AOB=90°,矩形CDEF的顶点C、D、F分别在边AO、OB、AB上。
(1)如图1,若C、D恰好是边AO、OB的中点,则此时矩形CDEF的面积为_________;
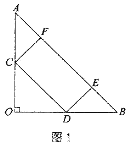
(2)如图2,若
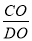 =
=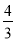 ,求矩形CDEF面积的最大值。
,求矩形CDEF面积的最大值。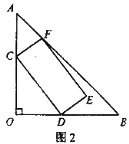
-
科目: 来源: 题型:
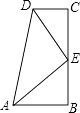
查看答案和解析>>【题目】已知如图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC,∠CED=35°,则∠EAB是度.
相关试题

