【题目】在△AOB中,OA=OB=8,∠AOB=90°,矩形CDEF的顶点C、D、F分别在边AO、OB、AB上。
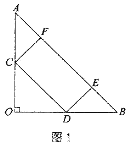
(1)如图1,若C、D恰好是边AO、OB的中点,则此时矩形CDEF的面积为_________;
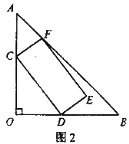
(2)如图2,若![]() =
=![]() ,求矩形CDEF面积的最大值。
,求矩形CDEF面积的最大值。
参考答案:
【答案】(1)S矩形CDEF=16;
(2)矩形CDEF面积的最大值为![]() 。
。
【解析】试题分析:(1)因为当C、D是边AO,OB的中点时,点E、F都在边AB上,且CF⊥AB,所以可求出CD的值,进而求出CF的值,矩形CDEF的面积可求出;
(2)设CD=x,CF=y.过F作FH⊥AO于H.在 Rt△COD中,用含x和y的代数式分别表示出CO、AH的长,进而表示出矩形CDEF的面积,再配方可求出面积的最大值.
试题解析:
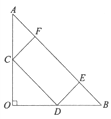
(1)如图,当C、D是边AO,OB的中点时,
点E、F都在边AB上,且CF⊥AB。
∵OA=OB=8,
∴OC=AC=OD=4。
∵∠AOB=90°,
∴CD=4![]() 。
。
在Rt△ACF中,
∵∠A=45°,
∴CF=2![]() ,
,
∴S矩形CDEF=4![]() ×2
×2![]() =16。
=16。
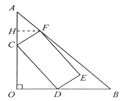
(2)设CD=x,CF=y。过F作FH⊥AO于H。在Rt△COD中,
∵tan∠CDO=![]() ,
,
∴sin∠CDO=![]() ,cos∠CDO=
,cos∠CDO=![]() ,
,
∴CO=![]() x
x
∵∠FCH+∠OCD=90°,
∴∠FCH+∠CDO,
∴HC=y·cos∠FCH=![]() y,
y,
∴FH=![]() y。
y。
∵△AHF是等腰直角三角形,
∴AH=FH=![]() y,
y,
∴AO=AH+HC+CO。
∴![]() ,
,
∴y=![]() (40-4x)
(40-4x)
易知S矩形CDEF=xy=![]()
![]() [(x-5)2-25],
[(x-5)2-25],
∴当x=5时,矩形CDEF面积的最大值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数y=
 的图象如图所示,则一元二次方程x2-(2k-1)x+k2-1=0根的情况是( )
的图象如图所示,则一元二次方程x2-(2k-1)x+k2-1=0根的情况是( )
A. 没有实根 B. 有两个不等实根 C. 有两个相等实根 D. 无法确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O是直线AB上一点,OC为任一条射线,OM平分∠AOC,ON平分∠BOC.
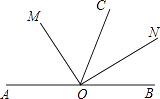
(1)图中与∠AON互补的角有;
(2)猜想∠MON的度数为 , 试说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b,c,是△ABC的三边,且满足a2b﹣a2c=b3﹣b2c,则△ABC的形状为( )
A. 等腰三角形 B. 直角三角形 C. 等边三角形 D. 任意三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC,∠CED=35°,则∠EAB是度.
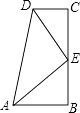
-
科目: 来源: 题型:
查看答案和解析>>【题目】若A、B两点在数轴上所表示的数分别为a、b,则A、B两点间的距离可记为|a﹣b|:
(1)如图:若A、B两点在数轴上所表示的数分别为﹣2、4,求A、B两点的距离为;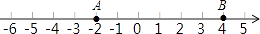
(2)若A,B两点分别以每秒3个单位长度和每秒1个单位长度的速度同时沿数轴正方向运动,设运动时间为t秒,解答下列问题:
①运动t秒后,A点所表示的数为 , B点所表示的数为;(答案均用含t的代数式表示)
②当t为何值时,A、B两点的距离为4? -
科目: 来源: 题型:
查看答案和解析>>【题目】有理数a,b,c在数轴上的位置如图所示,化简:|b﹣a|﹣|c﹣b|+|a+b|.
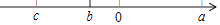
相关试题

