【题目】如图△ABC为等边三角形,直线a∥AB,D为直线BC上一点,∠ADE交直线a于点E,且∠ADE=60°.
(1)若D在BC上(如图1)求证CD+CE=CA;

(2)若D在CB延长线上,CD、CE、CA存在怎样数量关系,给出你的结论并证明.
参考答案:
【答案】(1)证明见解析;(2)CD、CE、CA满足CE+CA=CD,证明见解析.
【解析】
(1)实际上也就是求两条线段相等,在AC上取一点F,使CF=CD,然后求证△ADF≌△EDC即可;(2)归根究底仍是求两条线段的问题,通过求证全等,最终得出几条边之间的关系.
(1)证明:在AC上取点F,使CF=CD,连接DF.
∵∠ACB=60°,
∴△DCF为等边三角形.
∴∠3+∠4=∠4+∠5=60°.
∴∠3=∠5.
∵∠1+∠ADE=∠2+∠ACE,
∴∠1=∠2.
在△ADF和△EDC中,
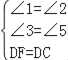 ,
,
∴△ADF≌△EDC(AAS).
∴CE=AF.
∴CD+CE=CF+AF=CA.
(2)解:CD、CE、CA满足CE+CA=CD;
证明:
在CA延长线上取CF=CD,连接DF.
∵△ABC为等边三角形,
∴∠ACD=60°,
∵CF=CD,
∴△FCD为等边三角形.
∵∠1+∠2=60°,
∵∠ADE=∠2+∠3=60°,
∴∠1=∠3.
在△DFA和△DCE中
 ,
,
∴△DFA≌△DCE(ASA).
∴AF=CE.
∴CE+CA=FA+CA=CF=CD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.一个游戏的中奖概率是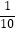 ,则做10次这样的游戏一定会中奖
,则做10次这样的游戏一定会中奖
B.一组数据6,8,7,8,8,9,10的众数和中位数都是8
C.为了解全国中学生的心理健康情况,应该采用普查的方式
D.若甲组数据的方差S2甲=0.01,乙组数据的方差S2乙=0.1,则乙组数据比甲组数据稳定 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,一个四边形纸片ABCD,∠B=∠D=90°,把纸片按如图所示折叠,使点B落在AD边上的B'点,AE是折痕。

(1)试判断B'E与DC的位置关系并说明理由。
(2)如果∠C=130°,求∠AEB的度数。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为6的菱形ABCD中,∠DAB=60°,以点D为圆心,菱形的高DF为半径画弧,交AD于点E,交CD于点G,则图中阴影部分的面积是( )

A.18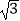 ﹣9π
﹣9π
B.18﹣3π
C.9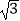 ﹣
﹣ 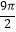
D.18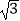 ﹣3π
﹣3π -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A、B、C、D、E在同一直线上,且AC=BD,E是线段BC的中点.

(1)点E是线段AD的中点吗?说明理由;
(2)当AD=10,AB=3时,求线段BE的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为( )

A.
B.2
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列等式
12=1= ×1×2×(2+1)
×1×2×(2+1)
12+22= ×2×3×(4+1)
×2×3×(4+1)
12+22+32= ×3×4×(6+1)
×3×4×(6+1)
12+22+32+42= ×4×5×(8+1)…
×4×5×(8+1)…
可以推测12+22+32+…+n2= .
相关试题

