【题目】计算题:(1)12﹣18+7﹣15;
(2)![]() ×(﹣7)﹣(﹣13)×(﹣
×(﹣7)﹣(﹣13)×(﹣![]() );
);
(3)![]() ;
;
(4)(-3)×(-![]() )÷(-1
)÷(-1![]() );
);
(5)-19![]() ×8;
×8;
(6)﹣12﹣![]() ×[(﹣2)3+(﹣3)2].
×[(﹣2)3+(﹣3)2].
参考答案:
【答案】(1)﹣14;(2)﹣15;(3)5;(4)-2;(5)-158;(6)![]() .
.
【解析】
(1)原式利用减法法则变形,计算即可得到结果;
(2)原式先计算乘法,再相加即可得到结果;
(3)原式利用乘法分配律即可得到结果;
(4)原式利用除法法则变形,约分即可得到结果;
(5)原式利用乘法法则即可得到结果;
(6)原式先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果.;
解:(1)12﹣18+7﹣15=﹣14;
(2)![]() ×(﹣7)﹣(﹣13)×(﹣
×(﹣7)﹣(﹣13)×(﹣![]() )
)
=![]() ×(﹣7)﹣13×
×(﹣7)﹣13×![]()
=![]() ×(﹣7﹣13)
×(﹣7﹣13)
=![]() ×(﹣20)
×(﹣20)
=﹣15;
(3)![]()
=﹣![]() ×(﹣60)﹣
×(﹣60)﹣![]() ×(﹣60)+
×(﹣60)+![]() ×(﹣60)
×(﹣60)
=30+20﹣45
=5;
(4)(-3)×(- ![]() )÷(-1
)÷(-1![]() )
)
=-3![]() =-2
=-2
(5)-19![]() ×8
×8
=(-20+![]() )
)![]()
=-20![]()
=-160+2=-158
(6)﹣12﹣![]() ×[(﹣2)3+(﹣3)2]
×[(﹣2)3+(﹣3)2]
=﹣1﹣![]() ×[(﹣8)+9]
×[(﹣8)+9]
=﹣1﹣![]() ×1
×1
=﹣1﹣![]()
=﹣1![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某服装店用4500元购进一批衬衫,很快售完,服装店老板又用2100元购进第二批该款式的衬衫,进货量是第一次的一半,但进价每件比第一批降低了10元.
(1)这两次各购进这种衬衫多少件?
(2)若第一批衬衫的售价是200元/件,老板想让这两批衬衫售完后的总利润不低于2100元,则第二批衬衫每件至少要售多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】探索勾股定理时,我们发现“用不同的方式表示同一图形的面积”可以解决线段和(或差)的有关问题,这种方法称为面积法.请你运用面积法求解下列问题:在等腰△ABC中,AB=AC,BD为腰AC上的高.
(1)若BD=h,M是直线BC上的任意一点,M到AB、AC的距离分别为h1,h2.
A、若M在线段BC上,请你结合图形①证明:h1+h2=h;
B、当点M在BC的延长线上时,h1,h2,h之间的关系为 .(请直接写出结论,不必证明)
(2)如图②,在平面直角坐标系中有两条直线l1:y=
 x+6;l2:y=﹣3x+6.若l2上的一点M到l1的距离是2,请你利用以上结论求解点M的坐标.
x+6;l2:y=﹣3x+6.若l2上的一点M到l1的距离是2,请你利用以上结论求解点M的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)(学习心得)
小刚同学在学习完“圆”这一章内容后,感觉到一些几何问题,如果添加辅助圆,运用圆的知识解决,可以使问题变得非常容易.
例如:如图
 ,在
,在 中,
中, ,
, ,
, 是
是 外一点,且
外一点,且 ,求
,求 的度数,若以点
的度数,若以点 为圆心,
为圆心, 为半径作辅助圆⊙
为半径作辅助圆⊙ ,则点
,则点 、
、 必在⊙
必在⊙ 上,
上, 是⊙
是⊙ 的圆心角,而
的圆心角,而 是圆周角,从而可容易得到
是圆周角,从而可容易得到 __________
__________ .
.(2)(问题解决)
如图
 ,在四边形
,在四边形 中,
中, ,
, ,求
,求 的度数.
的度数.小刚同学认为用添加辅助圆的方法,可以使问题快速解决,他是这样思考的:
 的外接圆就是以
的外接圆就是以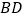 的中点为圆心,
的中点为圆心, 长为半径的圆;
长为半径的圆; 的外接圆也是以
的外接圆也是以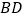 的中点为圆心,
的中点为圆心, 长为半径的圆.这样
长为半径的圆.这样 、
、 、
、 、
、 四点在同一个圆上,进而可以利用圆周角的性质求出
四点在同一个圆上,进而可以利用圆周角的性质求出 的度数,请运用小刚的思路解决这个问题.
的度数,请运用小刚的思路解决这个问题.(3)(问题拓展)
如图
 ,在
,在 中,
中, ,
, 是
是 边上的高,且
边上的高,且 ,
, ,求
,求 的长.
的长.
-
科目: 来源: 题型:
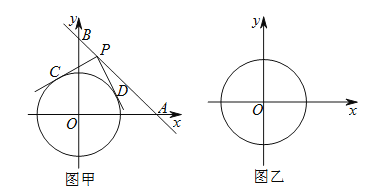
查看答案和解析>>【题目】如图甲,在平面直角坐标系中,直线分别交
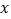 轴、
轴、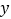 轴于点
轴于点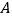 、
、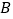 ,⊙
,⊙ 的半径为
的半径为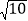 个单位长度,点
个单位长度,点 为直线
为直线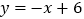 上的动点,过点
上的动点,过点 作⊙
作⊙ 的切线
的切线 、
、 ,切点分别为
,切点分别为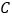 、
、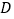 ,且
,且 .
.
(1)判断四边形
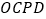 的形状并说明理由.
的形状并说明理由.(2)求点
 的坐标.
的坐标.(3)若直线
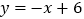 沿
沿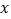 轴向左平移得到一条新的直线
轴向左平移得到一条新的直线 ,此直线将⊙
,此直线将⊙ 的圆周分得两段弧长之比为
的圆周分得两段弧长之比为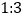 ,请直接写出
,请直接写出 的值.
的值.(4)若将⊙
 沿
沿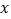 轴向右平移(圆心
轴向右平移(圆心 始终保持在
始终保持在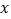 轴上),试写出当⊙
轴上),试写出当⊙ 与直线
与直线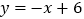 有交点时圆心
有交点时圆心 的横坐标
的横坐标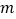 的取值范围.(直接写出答案)
的取值范围.(直接写出答案) -
科目: 来源: 题型:
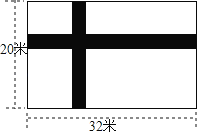
查看答案和解析>>【题目】如图所示,宽为20米,长为32米的长方形地面上,修筑宽度为x米的两条互相垂直的小路,余下的部分作为耕地,如果要在耕地上铺上草皮,选用草皮的价格是每平米a元,
(1)求买草皮至少需要多少元?(用含a,x的式子表示)
(2)计算a=40,x=2时,草皮的费用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数填入它所属的集合内:
3,200%,
 ,|2|,0,5.32,2.333….
,|2|,0,5.32,2.333….(1)整数集合:

 ;
;(2)分数集合:

 ;
;(3)非负数集合:

 ;
;
相关试题

