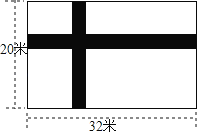
【题目】如图所示,宽为20米,长为32米的长方形地面上,修筑宽度为x米的两条互相垂直的小路,余下的部分作为耕地,如果要在耕地上铺上草皮,选用草皮的价格是每平米a元,
(1)求买草皮至少需要多少元?(用含a,x的式子表示)
(2)计算a=40,x=2时,草皮的费用.
参考答案:
【答案】(1)(640-52x+ x2)a;(2)21600元.
【解析】
(1)先求出小路的面积,再用总面积减去小路面积,得到耕地面积,再乘以草皮的价格即可得出答案;
(2)把a=40,x=2代入(1)中的代数式,即可求出草皮的费用.
解:(1)依题意,得
32x+(20-x)x=32x+20x-x2=52x-x2(平方米),32×20-(52x-x2)=640-52x+ x2
所以买草皮至少需要(640-52x+ x2)a元;
(2)当a=40,x=2时,
(640-52x+ x2)a =(640-52×2+22)×40=21600(元).
所以当a=40,x=2时,草皮的费用是21600元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)(学习心得)
小刚同学在学习完“圆”这一章内容后,感觉到一些几何问题,如果添加辅助圆,运用圆的知识解决,可以使问题变得非常容易.
例如:如图
 ,在
,在 中,
中, ,
, ,
, 是
是 外一点,且
外一点,且 ,求
,求 的度数,若以点
的度数,若以点 为圆心,
为圆心, 为半径作辅助圆⊙
为半径作辅助圆⊙ ,则点
,则点 、
、 必在⊙
必在⊙ 上,
上, 是⊙
是⊙ 的圆心角,而
的圆心角,而 是圆周角,从而可容易得到
是圆周角,从而可容易得到 __________
__________ .
.(2)(问题解决)
如图
 ,在四边形
,在四边形 中,
中, ,
, ,求
,求 的度数.
的度数.小刚同学认为用添加辅助圆的方法,可以使问题快速解决,他是这样思考的:
 的外接圆就是以
的外接圆就是以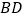 的中点为圆心,
的中点为圆心, 长为半径的圆;
长为半径的圆; 的外接圆也是以
的外接圆也是以 的中点为圆心,
的中点为圆心, 长为半径的圆.这样
长为半径的圆.这样 、
、 、
、 、
、 四点在同一个圆上,进而可以利用圆周角的性质求出
四点在同一个圆上,进而可以利用圆周角的性质求出 的度数,请运用小刚的思路解决这个问题.
的度数,请运用小刚的思路解决这个问题.(3)(问题拓展)
如图
 ,在
,在 中,
中, ,
, 是
是 边上的高,且
边上的高,且 ,
, ,求
,求 的长.
的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题:(1)12﹣18+7﹣15;
(2)
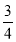 ×(﹣7)﹣(﹣13)×(﹣
×(﹣7)﹣(﹣13)×(﹣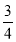 );
);(3)
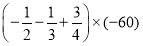 ;
;(4)(-3)×(-
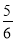 )÷(-1
)÷(-1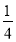 );
);(5)-19
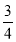 ×8;
×8;(6)﹣12﹣
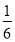 ×[(﹣2)3+(﹣3)2].
×[(﹣2)3+(﹣3)2]. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图甲,在平面直角坐标系中,直线分别交
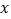 轴、
轴、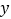 轴于点
轴于点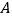 、
、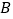 ,⊙
,⊙ 的半径为
的半径为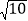 个单位长度,点
个单位长度,点 为直线
为直线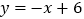 上的动点,过点
上的动点,过点 作⊙
作⊙ 的切线
的切线 、
、 ,切点分别为
,切点分别为 、
、 ,且
,且 .
.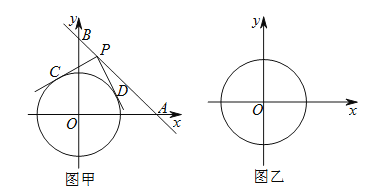
(1)判断四边形
 的形状并说明理由.
的形状并说明理由.(2)求点
 的坐标.
的坐标.(3)若直线
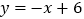 沿
沿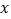 轴向左平移得到一条新的直线
轴向左平移得到一条新的直线 ,此直线将⊙
,此直线将⊙ 的圆周分得两段弧长之比为
的圆周分得两段弧长之比为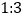 ,请直接写出
,请直接写出 的值.
的值.(4)若将⊙
 沿
沿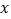 轴向右平移(圆心
轴向右平移(圆心 始终保持在
始终保持在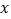 轴上),试写出当⊙
轴上),试写出当⊙ 与直线
与直线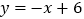 有交点时圆心
有交点时圆心 的横坐标
的横坐标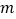 的取值范围.(直接写出答案)
的取值范围.(直接写出答案) -
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数填入它所属的集合内:
3,200%,
 ,|2|,0,5.32,2.333….
,|2|,0,5.32,2.333….(1)整数集合:

 ;
;(2)分数集合:

 ;
;(3)非负数集合:

 ;
; -
科目: 来源: 题型:
查看答案和解析>>【题目】教师节当天,出租车司机小王在东西向的街道上免费接送教师,规定向东为正,向西为负,当天出租车的行程如下(单位:千米)
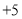 ,
,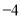 ,
,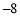 ,
,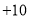 ,
,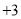 ,
,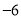 ,
,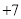 ,
,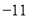 .
.(1)将最后一名老师送到目的地时,小王距出发地多少千米?
(2)若汽车耗油量为0.5升/千米,则当天耗油多少升?若汽油价格为6.70元/升,则小王共花费了多少元钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列两个等式:
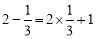 ,
, ,给出定义如下:我们称使等式
,给出定义如下:我们称使等式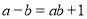 成立的一对有理数“
成立的一对有理数“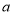 ,
, ”为“共生有理数对”,记为(
”为“共生有理数对”,记为(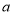 ,
, ).
).(1)通过计算判断数对“2,1,“4,
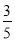 ”是不是“共生有理数对”;
”是不是“共生有理数对”;(2)若(6,a)是“共生有理数对”,求a的值;
(3)若(m,n)是“共生有理数对”,则“n,m”___“共生有理数对”(填“是”或“不是”),并说明理由;
相关试题

