【题目】探索勾股定理时,我们发现“用不同的方式表示同一图形的面积”可以解决线段和(或差)的有关问题,这种方法称为面积法.请你运用面积法求解下列问题:在等腰△ABC中,AB=AC,BD为腰AC上的高.
(1)若BD=h,M是直线BC上的任意一点,M到AB、AC的距离分别为h1,h2.
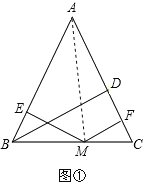
A、若M在线段BC上,请你结合图形①证明:h1+h2=h;
B、当点M在BC的延长线上时,h1,h2,h之间的关系为 .(请直接写出结论,不必证明)
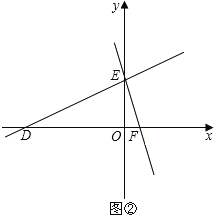
(2)如图②,在平面直角坐标系中有两条直线l1:y=![]() x+6;l2:y=﹣3x+6.若l2上的一点M到l1的距离是2,请你利用以上结论求解点M的坐标.
x+6;l2:y=﹣3x+6.若l2上的一点M到l1的距离是2,请你利用以上结论求解点M的坐标.

参考答案:
【答案】(1)A、证明见解析;B、h1﹣h2=h;(2)点M的坐标为![]() 或
或![]() .
.
【解析】
(1)A、如图,连接AM,设BD=h,EM=h1,MF=h2,由于S△ABC=S△ABM+S△ACM,而EM⊥AB,MF⊥AC,BD⊥AC,因此得到![]() ACh=
ACh=![]() ABh1+
ABh1+![]() ACh2,而AB=AC,因此即可证明结论;
ACh2,而AB=AC,因此即可证明结论;
B、可采用和A类似的方法,画图作辅助线,利用三角形面积公式根据S△ABC=S△ABM-S△ACM,代入化简得出h1-h2=h;
(2)由题意可知,DE=DF=10,所以△EDF是等腰三角形,
当点M在线段EF上时,依据(1)中结论,由h=EO=6可以得到M到DF(即x轴)的距离也为4,此时可求得M的坐标;
当点M在射线FE上时,依据(1)中结论,由h=EO=6可以得到M到DF(即x轴)的距离也为8,此时可求得M的坐标.
(1)证明:连接AM,
A、∵S△ABC=S△ABM+S△ACM,EM⊥AB,MF⊥AC,BD⊥AC,
∴![]() ACh=
ACh=![]() ABh1+
ABh1+![]() ACh2,
ACh2,
又∵AB=AC,
∴h=h1+h2;
B、结论:h=h1-h2.
理由:如图,连接MA,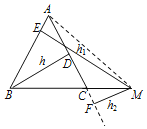
∵S△ABC=![]() ACBD=
ACBD=![]() ACh,
ACh,
S△ABM=![]() ABME=
ABME=![]() ABh1,
ABh1,
S△ACM=![]() ACMF=
ACMF=![]() ACh2,.
ACh2,.
又∵S△ABC=S△ABM-S△ACM,
∴![]() ACh=
ACh=![]() ABh1-
ABh1-![]() ACh2.
ACh2.
∵AB=AC,
∴h=h1-h2;
(2)由题意可知,DE=DF=10,
∴△EDF是等腰三角形,
当点M在线段EF上时,依据(1)中结论,
∵h=EO=6,
∴M到DF(即x轴)的距离为6-2=4,
∴点M的纵坐标为4,此时可求得M![]() ,
,
当点M在射线FE上时,依据(1)中结论,
∵h=EO=6,∴M到DF(即x轴)的距离为8,
∴点M的纵坐标为8,此时可求得M![]() ,
,
故点M的坐标为![]() 或
或![]() .
.
故答案为:(1)A、证明见解析;B、h1﹣h2=h;(2)点M的坐标为![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AE是∠BAC的角平分线,交BC于点E,DE∥AB交AC于点D.
(1)求证AD=ED;
(2)若AC=AB,DE=3,求AC的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, .
.
(1)先作
 的平分线交
的平分线交 边于点
边于点 ,再以点
,再以点 为圆心,
为圆心, 长为半径作⊙
长为半径作⊙ .
.(要求:尺规作图,保留作图痕迹,不写作法)
(2)请你判断(1)中
 与⊙
与⊙ 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.(3)若
 ,
, ,求出(1)中⊙
,求出(1)中⊙ 的半径.
的半径. -
科目: 来源: 题型:
查看答案和解析>>【题目】某服装店用4500元购进一批衬衫,很快售完,服装店老板又用2100元购进第二批该款式的衬衫,进货量是第一次的一半,但进价每件比第一批降低了10元.
(1)这两次各购进这种衬衫多少件?
(2)若第一批衬衫的售价是200元/件,老板想让这两批衬衫售完后的总利润不低于2100元,则第二批衬衫每件至少要售多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)(学习心得)
小刚同学在学习完“圆”这一章内容后,感觉到一些几何问题,如果添加辅助圆,运用圆的知识解决,可以使问题变得非常容易.
例如:如图
 ,在
,在 中,
中, ,
, ,
, 是
是 外一点,且
外一点,且 ,求
,求 的度数,若以点
的度数,若以点 为圆心,
为圆心, 为半径作辅助圆⊙
为半径作辅助圆⊙ ,则点
,则点 、
、 必在⊙
必在⊙ 上,
上, 是⊙
是⊙ 的圆心角,而
的圆心角,而 是圆周角,从而可容易得到
是圆周角,从而可容易得到 __________
__________ .
.(2)(问题解决)
如图
 ,在四边形
,在四边形 中,
中, ,
, ,求
,求 的度数.
的度数.小刚同学认为用添加辅助圆的方法,可以使问题快速解决,他是这样思考的:
 的外接圆就是以
的外接圆就是以 的中点为圆心,
的中点为圆心, 长为半径的圆;
长为半径的圆; 的外接圆也是以
的外接圆也是以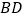 的中点为圆心,
的中点为圆心, 长为半径的圆.这样
长为半径的圆.这样 、
、 、
、 、
、 四点在同一个圆上,进而可以利用圆周角的性质求出
四点在同一个圆上,进而可以利用圆周角的性质求出 的度数,请运用小刚的思路解决这个问题.
的度数,请运用小刚的思路解决这个问题.(3)(问题拓展)
如图
 ,在
,在 中,
中, ,
, 是
是 边上的高,且
边上的高,且 ,
, ,求
,求 的长.
的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题:(1)12﹣18+7﹣15;
(2)
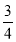 ×(﹣7)﹣(﹣13)×(﹣
×(﹣7)﹣(﹣13)×(﹣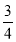 );
);(3)
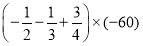 ;
;(4)(-3)×(-
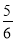 )÷(-1
)÷(-1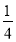 );
);(5)-19
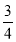 ×8;
×8;(6)﹣12﹣
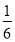 ×[(﹣2)3+(﹣3)2].
×[(﹣2)3+(﹣3)2]. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图甲,在平面直角坐标系中,直线分别交
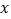 轴、
轴、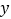 轴于点
轴于点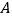 、
、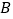 ,⊙
,⊙ 的半径为
的半径为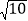 个单位长度,点
个单位长度,点 为直线
为直线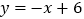 上的动点,过点
上的动点,过点 作⊙
作⊙ 的切线
的切线 、
、 ,切点分别为
,切点分别为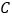 、
、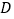 ,且
,且 .
.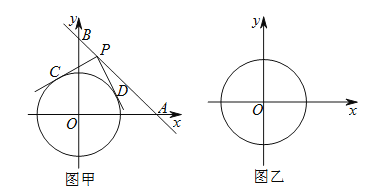
(1)判断四边形
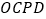 的形状并说明理由.
的形状并说明理由.(2)求点
 的坐标.
的坐标.(3)若直线
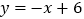 沿
沿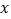 轴向左平移得到一条新的直线
轴向左平移得到一条新的直线 ,此直线将⊙
,此直线将⊙ 的圆周分得两段弧长之比为
的圆周分得两段弧长之比为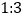 ,请直接写出
,请直接写出 的值.
的值.(4)若将⊙
 沿
沿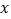 轴向右平移(圆心
轴向右平移(圆心 始终保持在
始终保持在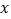 轴上),试写出当⊙
轴上),试写出当⊙ 与直线
与直线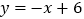 有交点时圆心
有交点时圆心 的横坐标
的横坐标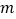 的取值范围.(直接写出答案)
的取值范围.(直接写出答案)
相关试题

