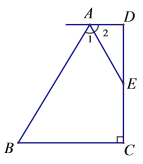
【题目】如图,已知AD∥BC,DC⊥BC, AE平分∠BAD, E为CD中点,试探索AD、BC和AB之间有何关系?并说明理由.
参考答案:
【答案】AD+BC=AB见解析;
【解析】
利用“AAS”可证明Rt△ADE≌Rt△AFE得到AD=AF,利用“HL”可证明Rt△BCE≌Rt△BFE得到BC=BF,于是有AD+BC=AF+BF=AB.
证明:过点E作EF⊥AB,连接BE
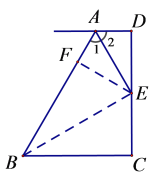
∵AD∥BC,DC⊥BC, EF⊥AB
∴∠D+∠C=180°,∠C=∠AFE=∠BFE=90°
∴∠D=∠AFE =90°.
∵AE平分∠BAD,
∴∠1=∠2
在△ADE和△AFE中
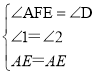
∴△ADE≌△AFE(AAS),
∴FE=DE,AD=AF
又∵E为CD中点
∴DE=CE,
∴FE =CE,
在Rt△BEF和Rt△BEC中,![]()
![]()
∴Rt△ BEF≌Rt△ BEC(HL),
∴BF= BC
∴AD+BC=AF+BF=AB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合与实践
图1是一个长为
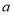 ,宽为
,宽为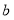 的长方形.现有相同的长方形若干,进行如下操作:
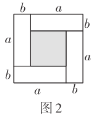
的长方形.现有相同的长方形若干,进行如下操作:(1)用四块图1的小长方形不重叠地拼成一个如图2所示的正方形.请利用图2中阴影部分面积的不同表示方法,直接写出代数式
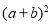 ,
,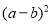 ,
,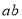 之间的等量关系___________;
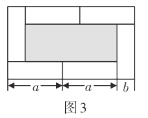
之间的等量关系___________;(2)将六块图1的小长方形不重叠地拼成一个如图3所示的长方形,通过不同方法计算阴影部分的面积,你能得到什么等式?请写出你的结论并用乘法法则证明这个等式成立;
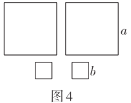
(3)现有图1的小长方形若干个,图4边长为
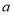 的正方形两个,边长为
的正方形两个,边长为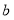 的正方形两个请你用这些图形拼成一个长方形(不重叠),使其面积为
的正方形两个请你用这些图形拼成一个长方形(不重叠),使其面积为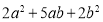 .画出你所拼成的长方形,并写出长方形的长和宽分别为多少.
.画出你所拼成的长方形,并写出长方形的长和宽分别为多少.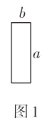
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB⊥BC且AB=BC,DE⊥CD且DE=CD,请按照图中所标注的数据,计算图中实线所围成的图形的面积S是( )

A. 36B. 48C. 72D. 108
-
科目: 来源: 题型:
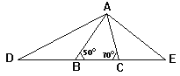
查看答案和解析>>【题目】如图,若△ABC的∠ABC=50°,∠ACB=70°,延长CB至点D,使BD=BA,延长BC至E点,使CE=CA, 连接AD、AE,则∠DAE的度数为__________度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】中秋节临近,某商场决定开展“金秋十月,回馈顾客”的让利活动,对部分品牌月饼进行打折销售,其中甲品牌月饼打八折,乙品牌月饼打七五折.已知打折前,买
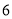 盒甲品牌月饼和
盒甲品牌月饼和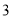 盒乙品牌月饼需
盒乙品牌月饼需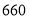 元;打折后,买
元;打折后,买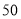 盒甲品牌月饼和
盒甲品牌月饼和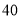 盒乙品牌月饼需
盒乙品牌月饼需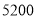 元.
元. (1)打折前甲、乙两种品牌月饼每盒分别为多少元?
(2)幸福敬老院需购买甲品牌月饼
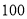 盒,乙品牌月饼
盒,乙品牌月饼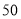 盒,问打折后购买这批月饼比不打折节省了多少钱?
盒,问打折后购买这批月饼比不打折节省了多少钱? -
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件中,发生的概率是
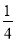 的是( )
的是( )A.从一副扑克牌中,任意抽取其中的一张,抽到红桃的概率
B.一个圆盘被染成红、黄、蓝、紫四种颜色,随机转动一次,转盘停止时,指针刚好指向红色的概率
C.小明开车到十字路口时,遇到红灯的概率
D.一道单选题有
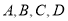 四个备用选项, 从中随机选一个作答,答对的概率
四个备用选项, 从中随机选一个作答,答对的概率 -
科目: 来源: 题型:
查看答案和解析>>【题目】在学习完“探索三角形全等的条件”一节后,小丽总结出很多全等三角形的模型,她设计了以下问题给同桌解决:做一个“
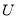 ”字形框架
”字形框架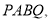 其中
其中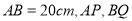 足够长,
足够长,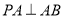 于点
于点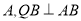 于点
于点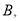 点
点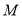 从
从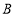 出发向
出发向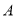 运动,点
运动,点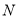 从
从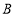 出发向
出发向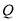 运动, 速度之比为
运动, 速度之比为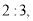 运动到某一瞬间两点同时停止,在
运动到某一瞬间两点同时停止,在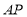 上取点
上取点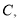 使
使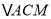 与
与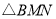 全等,则
全等,则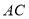 的长度为________________
的长度为________________
相关试题

