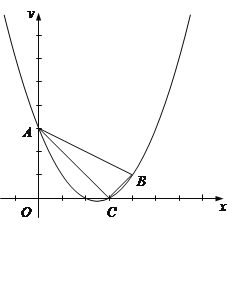
【题目】已知抛物线经过点![]() 、
、![]() 、
、![]() .
.
(1)求抛物线的解析式;
(2)联结AC、BC、AB,求![]() 的正切值;
的正切值;
(3)点P是该抛物线上一点,且在第一象限内,过点P作![]() 交
交![]() 轴于点
轴于点![]() ,当点
,当点![]() 在点
在点![]() 的上方,且
的上方,且![]() 与
与![]() 相似时,求点P的坐标.
相似时,求点P的坐标.
参考答案:
【答案】(1)![]() (2)
(2)![]() (3)点
(3)点![]() 的坐标为
的坐标为![]()
【解析】分析:(1)把A、B、C三点坐标带入抛物线解析式,利用待定系数法求解即可;
(2)由两点间的距离公式求得∴![]() 的长,由勾股定理的逆定理可判断
的长,由勾股定理的逆定理可判断![]() ,即可求得
,即可求得![]() 的值;
的值;
(3)当△APG与△ABC相似时,存在两种可能:∠PAG=∠CAB 和![]() ,分类讨论即可.
,分类讨论即可.
详解:(1)设所求二次函数的解析式为![]() ,
,
将![]() (
(![]() ,
,![]() )、
)、![]() (
(![]() ,
,![]() )、
)、![]() (
(![]() ,
,![]() )代入,得
)代入,得 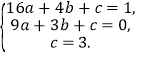
解得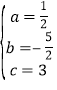 ,
,
所以,这个二次函数的解析式为![]() ;
;
(2)∵![]() (
(![]() ,
,![]() )、
)、![]() (
(![]() ,
,![]() )、
)、![]() (
(![]() ,
,![]() )
)
∴![]() ,
,![]() ,
,![]()
∴![]()
∴![]() ,
,
∴![]() ;
;
(3)过点P作![]() ,垂足为H,
,垂足为H,
设![]()
![]() ,则
,则![]()
![]()
∵![]() (
(![]() ,
,![]() )
)
∴![]() ,
,![]()
∵![]()
∴当△APG与△ABC相似时,存在以下两种可能:
1° ∠PAG=∠CAB 则![]()
即![]() ∴
∴![]() 解得
解得![]() ;
;
∴点 的坐标为
的坐标为![]() ;
;
2° ![]() ,则
,则![]()
即![]() ,
,
∴![]() ,解得
,解得![]() ,
,
∴点![]() 的坐标为
的坐标为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】温度通常有两种表示方法:华氏度(单位:℉)与摄氏度(单位:℃),已知华氏度数
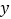 与摄氏度数
与摄氏度数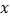 之间是一次函数关系,下表列出了部分华氏度与摄氏度之间的对应关系:
之间是一次函数关系,下表列出了部分华氏度与摄氏度之间的对应关系:摄氏度数
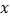 (℃)
(℃)…
0
…
35
…
100
…
华氏度数
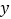 (℉)
(℉)…
32
…
95
…
212
…
(1)选用表格中给出的数据,求y关于x的函数解析式;
(2)有一种温度计上有两个刻度,即测量某一温度时左边是摄氏度,右边是华氏度,那么在多少摄氏度时,温度计上右边华氏度的刻度正好比左边摄氏度的刻度大56?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△AOB中,∠ABO=90°,OB=4,AB=8,直线y=-x+b分别交OA、AB于点C、D,且ΔBOD的面积是4.
(1)求直线AO的解析式;
(2)求直线CD的解析式;
(3)若点M是x轴上的点,且使得点M到点A和点C的距离之和最小,求点的坐标.
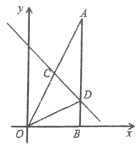
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,∠B=90°,AB=16cm,BC=12cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.
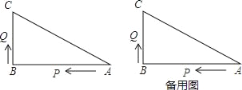
(1)出发2秒后,求PQ的长;
(2)当点Q在边BC上运动时,出发几秒钟后,△PQB能形成等腰三角形?
(3)当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在ABCD中,点E是BC的中点,连接AE并延长交DC的延长线于点F,连接BF.
(1)求证:△ABE≌△FCE;
(2)若AF=AD,求证:四边形ABFC是矩形.
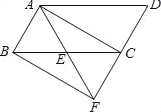
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解学生参加体育活动的情况,学校对学生进行随机抽样调查,其中一个问题是“你平均每天参加体育活动的时间是多少”,共有4个选项:A、1.5小时以上;B、1~1.5小时;C、0.5~1小时;D、0.5小时以下.图1、2是根据调查结果绘制的两幅不完整的统计图,请你根据统计图提供的信息,解答以下问题:
(1)本次一共调查了多少名学生?
(2)在图1中将选项B的部分补充完整;
(3)若该校有3000名学生,你估计全校可能有多少名学生平均每天参加体育活动的时间在0.5小时以下?
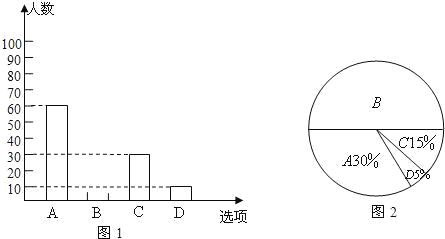
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P为边长为6的正方形ABCD的边BC上一动点(P与B、C不重合),Q在CD上,且CQ=BP,连接AP、BQ,将△BQC沿BQ所在的直线翻折得到△BQE,延长QE交BA的延长线于点F.
(1)试探究AP与BQ的数量与位置关系,并证明你的结论;
(2)当E是FQ的中点时,求BP的长。
相关试题

