【题目】如图,E,F是正方形ABCD的边AD上两个动点,满足AE=DF.连接CF交BD于点G,连接BE交AG于点H.若正方形的边长为2,则线段DH长度的最小值是 . 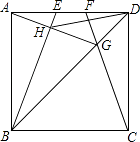
参考答案:
【答案】![]() ﹣1
﹣1
【解析】解:在正方形ABCD中,AB=AD=CD,∠BAD=∠CDA,∠ADG=∠CDG, 在△ABE和△DCF中,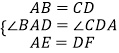 ,
,
∴△ABE≌△DCF(SAS),
∴∠1=∠2,
在△ADG和△CDG中,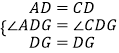 ,
,
∴△ADG≌△CDG(SAS),
∴∠2=∠3,
∴∠1=∠3,
∵∠BAH+∠3=∠BAD=90°,
∴∠1+∠BAH=90°,
∴∠AHB=180°﹣90°=90°,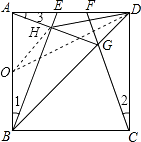
取AB的中点O,连接OH、OD,
则OH=AO= ![]() AB=1,
AB=1,
在Rt△AOD中,OD= ![]() =
= ![]() =
= ![]() ,
,
根据三角形的三边关系,OH+DH>OD,
∴当O、D、H三点共线时,DH的长度最小,
最小值=OD﹣OH= ![]() ﹣1.
﹣1.
(解法二:可以理解为点H是在Rt△AHB,AB直径的半圆 ![]() 上运动当O、H、D三点共线时,DH长度最小)
上运动当O、H、D三点共线时,DH长度最小)
故答案为: ![]() ﹣1.
﹣1.
根据正方形的性质可得AB=AD=CD,∠BAD=∠CDA,∠ADG=∠CDG,然后利用“边角边”证明△ABE和△DCF全等,根据全等三角形对应角相等可得∠1=∠2,利用“SAS”证明△ADG和△CDG全等,根据全等三角形对应角相等可得∠2=∠3,从而得到∠1=∠3,然后求出∠AHB=90°,取AB的中点O,连接OH、OD,根据直角三角形斜边上的中线等于斜边的一半可得OH= ![]() AB=1,利用勾股定理列式求出OD,然后根据三角形的三边关系可知当O、D、H三点共线时,DH的长度最小.
AB=1,利用勾股定理列式求出OD,然后根据三角形的三边关系可知当O、D、H三点共线时,DH的长度最小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.则下列结论:①△ABG≌△AFG;②BG=CG;③AG∥CF;④S△EGC=S△AFE;⑤∠AGB+∠AED=145°.其中正确的个数是( )

A. 2 B. 3 C. 4 D. 5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,将Rt△ABC绕A点逆时针旋转30°后得到Rt△ADE,点B经过的路径为
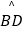 ,则图中阴影部分的面积是 .
,则图中阴影部分的面积是 . 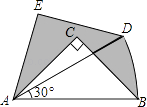
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)单项式﹣2x3ym与5xn+1y的差是一个单项式,求
 的值;
的值;(2)化简求值:(x2+5﹣4x3)﹣2(﹣2x3+5x﹣4),其中x=﹣2;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的两条对角线AC、BD相交于点O,延长BA至点F,使BF=AC,连接DF,∠DBA的平分线交DF于点P,连接PA.PO,如果AB=
 ,那么PA2+PO2=______.
,那么PA2+PO2=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小花家在装修客厅时,购进彩色地砖和原色地砖共120块,一共花费了8700元.已知原色地砖的价钱是60元/块,彩色地砖的价钱是110元/块.
(1)两种型号的地砖各采购了多少块?
(2)如果厨房也要铺这两种型号的地砖共70块,且采购费用不超过4400元,那么彩色地砖最多能采购多少块?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业前年按可回收垃圾处理费15元/吨、不可回收垃圾处理费25元/吨的收费标准,共支付两种垃圾处理费5000元,从去年元月起,收费标准上调为:可回收垃圾处理费30元/吨,不可回收垃圾处理费100元/吨.若该企业去年处理的这两种垃圾数量与前年相比没有变化,但调价后就要多支付处理费9000元.
(1)该企业前年处理的可回收垃圾和不可回收垃圾各多少吨?
(2)该企业计划今年将上述两种垃圾处理总量减少到200吨,且可回收垃圾不少于不可回收垃圾处理量的3倍,则今年该企业至少有多少吨可回收垃圾?
相关试题

