【题目】如图,正方形ABCD的两条对角线AC、BD相交于点O,延长BA至点F,使BF=AC,连接DF,∠DBA的平分线交DF于点P,连接PA.PO,如果AB=![]() ,那么PA2+PO2=______.
,那么PA2+PO2=______.

参考答案:
【答案】3-![]()
【解析】根据正方形的性质即可得出BD=AC=![]() AB=2,结合BF=AC即可得出点P为DF的中点,根据正方形的性质可得出点O为BD的中点以及∠BAD=90°,由此即可得出PO为△DFB的中位线,结合BF的长度即可求出PO的长度,再根据直角三角形斜边中线等斜边的一半结合勾股定理即可得出PA的长度,将其代入PA2+PO2中即可得出结论.
AB=2,结合BF=AC即可得出点P为DF的中点,根据正方形的性质可得出点O为BD的中点以及∠BAD=90°,由此即可得出PO为△DFB的中位线,结合BF的长度即可求出PO的长度,再根据直角三角形斜边中线等斜边的一半结合勾股定理即可得出PA的长度,将其代入PA2+PO2中即可得出结论.
∵四边形ABCD为正方形,BF=AC,AB=![]() ,∴BF=AC=
,∴BF=AC=![]() AB=2,BC=AD,
AB=2,BC=AD,
∴AF=BF-AB=2-![]() ,BF=BD.∵BP平分∠DBA, ∴点P为DF的中点.
,BF=BD.∵BP平分∠DBA, ∴点P为DF的中点.
∵四边形ABCD为正方形,对角线AC、BD相交于点O,
∴∠BAD=90°,点O为BD中点, ∴PO为△DFB的中位线,
∴PO=![]() BF=1, ∵∠DAF=180°-∠BAD=90°,点P为DF的中点,
BF=1, ∵∠DAF=180°-∠BAD=90°,点P为DF的中点,
∴PA=![]() DF=
DF=![]() , ∴
, ∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,将Rt△ABC绕A点逆时针旋转30°后得到Rt△ADE,点B经过的路径为
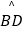 ,则图中阴影部分的面积是 .
,则图中阴影部分的面积是 . 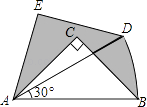
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)单项式﹣2x3ym与5xn+1y的差是一个单项式,求
 的值;
的值;(2)化简求值:(x2+5﹣4x3)﹣2(﹣2x3+5x﹣4),其中x=﹣2;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E,F是正方形ABCD的边AD上两个动点,满足AE=DF.连接CF交BD于点G,连接BE交AG于点H.若正方形的边长为2,则线段DH长度的最小值是 .
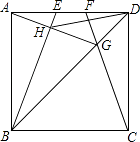
-
科目: 来源: 题型:
查看答案和解析>>【题目】小花家在装修客厅时,购进彩色地砖和原色地砖共120块,一共花费了8700元.已知原色地砖的价钱是60元/块,彩色地砖的价钱是110元/块.
(1)两种型号的地砖各采购了多少块?
(2)如果厨房也要铺这两种型号的地砖共70块,且采购费用不超过4400元,那么彩色地砖最多能采购多少块?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业前年按可回收垃圾处理费15元/吨、不可回收垃圾处理费25元/吨的收费标准,共支付两种垃圾处理费5000元,从去年元月起,收费标准上调为:可回收垃圾处理费30元/吨,不可回收垃圾处理费100元/吨.若该企业去年处理的这两种垃圾数量与前年相比没有变化,但调价后就要多支付处理费9000元.
(1)该企业前年处理的可回收垃圾和不可回收垃圾各多少吨?
(2)该企业计划今年将上述两种垃圾处理总量减少到200吨,且可回收垃圾不少于不可回收垃圾处理量的3倍,则今年该企业至少有多少吨可回收垃圾?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将二次函数y=x2﹣m(其中m>0)的图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,形成新的图象记为y1 , 另有一次函数y=x+b的图象记为y2 , 则以下说法: ①当m=1,且y1与y2恰好有三个交点时b有唯一值为1;
②当b=2,且y1与y2恰有两个交点时,m>4或0<m< ;
;
③当m=﹣b时,y1与y2一定有交点;
④当m=b时,y1与y2至少有2个交点,且其中一个为(0,m).
其中正确说法的序号为 .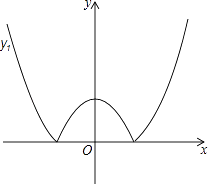
相关试题

