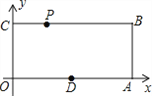
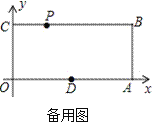
【题目】已知,如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在边BC上以每秒1个单位长的速度由点C向点B运动.
(1)当t为何值时,CP=OD?
(2)当△OPD为等腰三角形时,写出点P的坐标(请直接写出答案,不必写过程).
(3)在线段PB上是否存在一点Q,使得四边形ODQP为菱形?若存在,求t的值,并求出Q点的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)5;(2)(2,4),(2.5, 4),(3,4),(8, 4);(3)(8,4).
【解析】试题分析:
(1)由已知条件易得:OD=5,由CP=t=OD=5即可求得t的值;
(2)结合图形分:OP=DP、OP=OD和PD=OD三种情况分别讨论解答即可;
(3)由四边形ODQP是菱形可知:OP=OD=5,从而可求出点P此时的坐标,再由PQ=OD=5即可求得点Q的坐标.
试题解析:
(1)∵点A的坐标为(10,0),
∴OA=10,
∵点D是OA的中点,
∴OD=5,
又∵CP=t=OD=5,
∴t=5;
(2)点C的坐标为(0,4),CB∥![]() 轴,点P在CB上运动,
轴,点P在CB上运动,
∴点P的纵坐标为4.
△OPD为等腰三角形,存在以下三种情况:
I、当OP=DP时,点P在线段OD的垂直平分线上,
∴此时CP=t=![]() OD=2.5,
OD=2.5,
∴此时点P的坐标为(2.5,4);
II、当OP=OD=5时,
在Rt△OPC中,由勾股定理可得:CP=![]() ,
,
∴此时点P的坐标为(3,4);
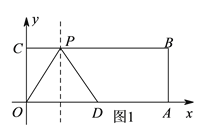
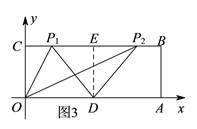
III、当PD=OD=5时,如图3,存在以下两种情况:
过点D作DE⊥BC于点E,则DE=OC=4,CE=OD=5,
在Rt△P1DE中,∵P1D=OD=5,
∴P1E=![]() ,
,
∴CP1=CE-P1E=2,即此时点P1的坐标为(2,4);
同理可得:点P2的坐标为(8,4);
综上所述,当△OPD为等腰三角形时,点P的坐标为(2,4)、(2.5,4)、(3,4)和(8,4);
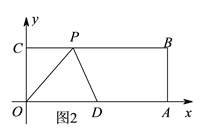
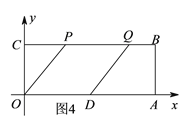
(3)如图4,∵四边形ODQP是菱形,
∴OP=OD=PQ=5,
由(2)可知,当OP=5时,CP=3,
∴CQ=CP+PQ=8,
又∵点P在线段CB上,
∴点Q的坐标为(8,4).
-
科目: 来源: 题型:
查看答案和解析>>【题目】地球上的海洋面积约为361000000km2,用科学记数法可表示为( )
A.361×106km2 B.36.1×107km2C.0.361×109km2D.3.61×108km2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是抛物线y=ax2+bx+c(a≠0),其顶点为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间,则下列结论正确的是( )

①若抛物线与x轴的另一个交点为(k,0),则-2<k<-1; ②c-a=n;
③若x<-m时,y随x的增大而增大,则m=-1;④若x<0时,ax2+(b+2)x<0.
A. ①②④ B. ①③④ C. ①② D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC的内切圆⊙O与两直角边AB、BC分别相切于点D、E,过劣弧
 (不包括端点D、E)上任一点作⊙O的切线MN与AB、BC分别交于点M、N.若AC=10,BC=6,则△MBN的周长为__.
(不包括端点D、E)上任一点作⊙O的切线MN与AB、BC分别交于点M、N.若AC=10,BC=6,则△MBN的周长为__.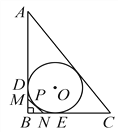
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△DAC和△EBC均是等边三角形,AE、BD分别与CD、CE交于点M、N,有如下结论:①△ACE≌△DCB;②CM=CN;③AC=DN;④∠DAE=∠DBC.其中正确的有( )

A. ②④ B. ①②③ C. ①②④ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】体育老师从七年级学生中抽取40名参加全校的健身操比赛.这些学生身高(单位:cm)的最大值为175,最小值为155.若取组距为3,则可以分成____组.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列算式中,结果等于a5的是( )
A. a2+a3 B. a2a3 C. a5÷a D. (a2)3
相关试题

