搜索
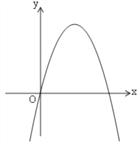
【题目】如图是抛物线y=ax2+bx+c（a≠0），其顶点为（1，n），且与x轴的一个交点在点（3，0）和（4，0）之间，则下列结论正确的是（ ）
①若抛物线与x轴的另一个交点为（k，0），则－2＜k＜－1； ②c－a=n；
③若x＜－m时，y随x的增大而增大，则m=－1；④若x＜0时，ax2+（b+2）x＜0.
A. ①②④ B. ①③④ C. ①② D. ①②③④
参考答案：
【答案】A
【解析】根据抛物线的顶点和与x轴的交点，其对称轴为x=-
=1，则b=-2a，可由抛物线与x轴的另一个交点为（k，0），则
或
，解得k=-1或k=-2，即－2＜k＜－1，故①正确；当x=1时，n=a+b+c，即a-2a+c=n，即c-a=n，故②正确；根据二次函数的增减性，可知当x＜1时，y随x增大而增大，可知m＜-1，故③不正确；由抛物线的开口向下，则a＜0，所以y=ax2+（b+2）x也开口向下，且过原点，因此当y=0时，ax2+（b+2）x=0，因式分解为x（ax+b+2）=0，所以x=0或x=
，所以y =ax2+（b+2）x=
＞0，如图，
所以当x＜0时，y=ax2+（b+2）x＜0，故④正确.
故选：A.
-
科目： 来源： 题型：
查看答案和解析>>【题目】小颖和小亮上山游玩，小颗乘坐缆车，小亮步行，两人相约在山顶的缆车终点会合.已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍，小颗在小亮出发后50分才乘上缆车，缆车的平均速度为180米/分，设小亮出发x分后行走的路程为y米。图中的折线表示小亮在整个行走过程中y随x的变化关系.
（1)小亮行走的总路程是_________米，他途中休息了___________分；
（2）分别求出小亮在休息前和休息后所走的路程段上的步行速度；
（3）当小颖到达缆车终点时，小亮离缆车终点的路程是多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：直线AB∥CD，点M，N分别在直线AB，CD上，点E为平面内一点.
(1)如图1，∠BME，∠E，∠END的数量关系为 (直接写出答案)；
(2)如图2，∠BME＝m°，EF平分∠MEN，NP平分∠END，EQ∥NP，求∠FEQ的度数(用用含m的式子表示)
(3)如图3，点G为CD上一点，∠BMN＝n·∠EMN，∠GEK＝n·∠GEM，EH∥MN交AB于点H，探究∠GEK，∠BMN，∠GEH之间的数量关系(用含n的式子表示)
-
科目： 来源： 题型：
查看答案和解析>>【题目】地球上的海洋面积约为361000000km2，用科学记数法可表示为（ ）
A.361×106km2 B.36.1×107km2C.0.361×109km2D.3.61×108km2
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，Rt△ABC的内切圆⊙O与两直角边AB、BC分别相切于点D、E，过劣弧
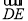(不包括端点D、E)上任一点作⊙O的切线MN与AB、BC分别交于点M、N.若AC=10，BC=6，则△MBN的周长为__.
-
科目： 来源： 题型：
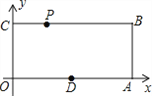
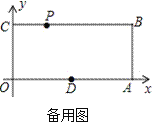
查看答案和解析>>【题目】已知，如图，O为坐标原点，四边形OABC为矩形，A（10，0），C（0，4），点D是OA的中点，点P在边BC上以每秒1个单位长的速度由点C向点B运动．
（1）当t为何值时，CP=OD？
（2）当△OPD为等腰三角形时，写出点P的坐标（请直接写出答案，不必写过程）．
（3）在线段PB上是否存在一点Q，使得四边形ODQP为菱形？若存在，求t的值，并求出Q点的坐标；若不存在，请说明理由.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△DAC和△EBC均是等边三角形，AE、BD分别与CD、CE交于点M、N，有如下结论：①△ACE≌△DCB；②CM=CN；③AC=DN；④∠DAE=∠DBC．其中正确的有（ ）
A. ②④ B. ①②③ C. ①②④ D. ①②③④
相关试题
