【题目】如图1,在△ABC中,AB=BC=5,AC=6,△ECD是△ABC沿BC方向平移得到的,连接AE、BE,且AC和BE相交于点O.
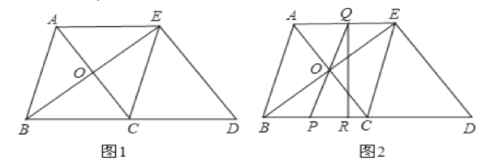
(1)求证:四边形ABCE是菱形;
(2)如图2,P是线段BC上一动点(不与B. C重合),连接PO并延长交线段AE于点Q,过Q作QR⊥BD交BD于R.
①四边形PQED的面积是否为定值?若是,请求出其值;若不是,请说明理由;
②以点P、Q、R为顶点的三角形与以点B. C. O为顶点的三角形是否可能相似?若可能,请求出线段BP的长;若不可能,请说明理由.
参考答案:
【答案】(1)见解析;(2)①24,②![]() ;
;
【解析】
(1)利用平移的性质以及菱形的判定得出即可;
(2)①首先过E作EF⊥BD交BD于F,则∠EFB=90°,证出△QOE≌△POB,利用QE=BP,得出四边形PQED的面积为定值;
②当∠QPR=∠BCO时,△PQR∽△CBO,此时有OP=OC=3,过O作OG⊥BC交BC于G,得出△OGC∽△BOC,利用相似三角形的性质得出CG的长,进而得出BP的长.
(1)证明:∵△ABC沿BC方向平移得到△ECD,
∴EC=AB,AE=BC,
∵AB=BC,
∴EC=AB=BC=AE,
∴四边形ABCE是菱形;
(2)①四边形PQED的面积是定值,理由如下:
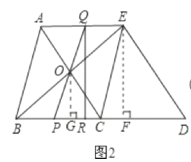
过E作EF⊥BD交BD于F,则∠EFB=90°,
∵四边形ABCE是菱形,
∴AE∥BC,OB=OE,OA=OC,OC⊥OB,
∵AC=6,
∴OC=3,
∵BC=5,
∴OB=4,sin∠OBC=![]() ,
,
∴BE=8,
∴EF=BEsin∠OBC=8×![]() ,
,
∵AE∥BC,
∴∠AEO=∠CBO,四边形PQED是梯形,
在△QOE和△POB中
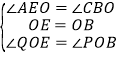 ,
,
∴△QOE≌△POB,
∴QE=BP,
∴S![]() =
=![]() (QE+PD)×EF=
(QE+PD)×EF=![]() (BP+DP)×EF=
(BP+DP)×EF=![]() ×BD×EF=
×BD×EF=![]() ×2BC×EF=BC×EF=5×
×2BC×EF=BC×EF=5×![]() =24;
=24;
②△PQR与△CBO可能相似,
∵∠PRQ=∠COB=90°,∠QPR>∠CBO,
∴当∠QPR=∠BCO时,△PQR∽△CBO,此时有OP=OC=3.
过O作OG⊥BC交BC于G.
∵∠OCB=∠OCB,∠OGC=∠BOC,
∴△OGC∽△BOC,
∴CG:CO=CO:BC,
即CG:3=3:5,
∴CG=![]() ,
,
∴BP=BCPC=BC2CG=52×![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明的父亲上星期五买进某公司股票1000股,每股30元,如表为本周内每日该股票的涨跌情况(单位:元)
星期
一
二
三
四
五
每股涨跌
+3
+1.5
-2
-1.5
+1
(1) 星期三收盘时,每股是多少元?
(2)本周内最高价是每股多少元?最低每股多少元?
(3)已知小明父亲买进股票时付了1.5‰的手续费,卖出时需付成交额1.5‰的手续费和1‰的交易税,如果他在周五收盘前将全部股票卖出,他的收益情况如何
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=ax+b的图象与反比例函数y=
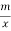 图象相交于点A(﹣1,2)与点B(﹣4,n).
图象相交于点A(﹣1,2)与点B(﹣4,n).(1)求一次函数和反比例函数的解析式;
(2)求△AOB的面积.
(3)在第二象限内,求不等式ax+b<
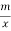 的解集(请直接写出答案).
的解集(请直接写出答案).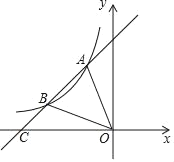
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠ACD=120°.
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为2,求图中阴影部分的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,图①、图②、图③均为顶点都在格点上的三角形(每个小方格的顶点叫格点),
(1)在图1中,图①经过一次 变换(填“平移”或“旋转”或“轴对称”)可以得到图②;
(2)在图1中,图③是可以由图②经过一次旋转变换得到的,其旋转中心是点 (填“A”或 “B”或“C”);
(3)在图2中画出图①绕点A顺时针旋转90°后的图④.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x,y的方程组
 ,则下列结论中正确的是_____
,则下列结论中正确的是_____①当a=5时,方程组的解是
 ;
;②当x,y值互为相反数时,a=20;
③当2x2y=16时,a=18;
④不存在一个实数a使得x=y.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在数轴上A点表示数
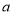 ,B点示数
,B点示数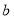 ,C点表示数
,C点表示数 ,
,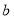 是最小的正整数,且
是最小的正整数,且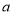 、
、 满足
满足 .
.
(1)
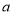 =__________,
=__________,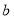 =__________,
=__________, =__________;
=__________;(2)若将数轴折叠,使得A点与C点重合,则点B与数__________表示的点重合;
(3)若点A、点B和点C分别以每秒2个单位、1个单位长度和4个单位长度的速度在数轴上同时向左运动,假设
 秒钟过后,A、B、C三点中恰有一点为另外两点的中点,求
秒钟过后,A、B、C三点中恰有一点为另外两点的中点,求 的值;
的值;(4)若点A、点B和点C分别以每秒2个单位、1个单位长度和4个单位长度的速度在数轴上同时向左运动时,小聪同学发现:当点C在B点右侧时,
 BC+3AB的值是个定值,求此时
BC+3AB的值是个定值,求此时 的值.
的值.
相关试题

