【题目】王威调查统计了他们家3月份每次打电话的通话时长,并将统计结果进行分组(每组含最小值,不含最大值) ,将分组后的结果绘制成如图所示的频数分布直方图,则下列说法中不正确的是( )
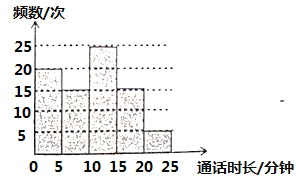
A.王威家3月份打电话的总频数为![]() 次
次
B.王威家3月份每次打电话的通话时长在![]() 这组的频数为
这组的频数为![]() 次
次
C.王威家3月份每次打电话的通话时长在![]() 这组的频数最多
这组的频数最多
D.王威家3月份每次打电话的通话时长在![]() 这组的频率为
这组的频率为![]()
参考答案:
【答案】D
【解析】
根据频数,总数,频率的定义即可判断.
解:A、正确.因为20+15+25+15+5=80故正确.
B、正确.由图象可知张浩家5月份每次打电话的通话时长在5-10分钟的频数为15次.故正确.
C、正确.由图象可知张浩家5月份每次打电话的通话时长在10-15分钟的频数最多.故正确.
D、错误.张浩家5月份每次打电话的通话时长在20-25分钟的频率为![]() .故错误.
.故错误.
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂新开发生产一种机器,每台机器成本y(万元)与生产数量x(台)之间满足一次函数关系(其中10≤x≤70,且为整数),函数y与自变量x的部分对应值如表
 (单位:台)
(单位:台)10
20
30
 (单位:万元/台)
(单位:万元/台)60
55
50
(1)求y与x之间的函数关系式;

(2)市场调查发现,这种机器每月销售量z(台)与售价a(万元/台)之间满足如图所示的函数关系.则当该厂第一个月生产的这种机器40台都按同一售价全部售出,请求出该厂第一个月销售这种机器的总利润.(注:利润=售价﹣成本)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在射线AB上顺次取两点C,D,使AC=CD=1,以CD为边作矩形CDEF,DE=2,将射线AB绕点A沿逆时针方向旋转,旋转角记为α(其中0°<α<45°),旋转后记作射线AB′,射线AB′分别交矩形CDEF的边CF,DE于点G,H.若CG=x,EH=y,则下列函数图象中,能反映y与x之间关系的是( )

A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB:y=-x-b分别与x、y轴交于A(6,0)、B两点,过点B的直线交x轴负半轴于点C,且OB:OC=3:1.
(1)求直线BC的解析式;
(2)如图,P为A点右侧x轴上的一动点,以P为直角顶点,BP为腰在第一象限内作等腰直角△BPQ,连接QA并延长交y轴于点K,当P点运动时,K点的位置是否发现变化?若不变,请求出它的坐标;如果变化,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中
 是原点,
是原点, 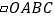 的顶点
的顶点  的坐标分别是
的坐标分别是 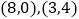 ,点
,点  把线段
把线段  三等分,延长
三等分,延长  分别交
分别交  于点
于点  ,连接
,连接  ,则下列结论:
,则下列结论:
① 是
是  的中点;②
的中点;②  与
与 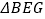 相似;③四边形
相似;③四边形  的面积是
的面积是  ;④
;④  ;其中正确的结论是 . (填写所有正确结论的序号)
;其中正确的结论是 . (填写所有正确结论的序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知平面直角坐标系中有一点

 点
点 到
到 轴的距离为
轴的距离为 时,求出点
时,求出点 的坐标;
的坐标; 点
点 的坐标为
的坐标为 ,且
,且 轴,求出点
轴,求出点 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,我们给中国象棋棋盘建立一个平面直角坐标系(每个小正方形的边长均为
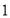 ),根据象棋中“马”走“日”的规定,若“马”的位置在图中的点
),根据象棋中“马”走“日”的规定,若“马”的位置在图中的点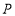

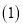 写出下一步“马”可能到达的点的坐标为_ (写出所有可能的点的坐标);
写出下一步“马”可能到达的点的坐标为_ (写出所有可能的点的坐标);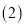 顺次连接
顺次连接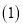 中的所有点,得到的图形是 _图形(填“中心对称”或“轴对称”;
中的所有点,得到的图形是 _图形(填“中心对称”或“轴对称”;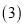 将
将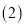 中得到的图形各顶点的坐标都乘以
中得到的图形各顶点的坐标都乘以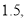 请在平面直角坐标系中画出变化后的图形,并与原图形比较,形状和大小有怎样的变化?
请在平面直角坐标系中画出变化后的图形,并与原图形比较,形状和大小有怎样的变化?
相关试题

