【题目】如图,直线AB:y=-x-b分别与x、y轴交于A(6,0)、B两点,过点B的直线交x轴负半轴于点C,且OB:OC=3:1.
(1)求直线BC的解析式;
(2)如图,P为A点右侧x轴上的一动点,以P为直角顶点,BP为腰在第一象限内作等腰直角△BPQ,连接QA并延长交y轴于点K,当P点运动时,K点的位置是否发现变化?若不变,请求出它的坐标;如果变化,请说明理由.

参考答案:
【答案】(1)y=3x+6(2)K点的位置不发生变化,K(0,6),理由见解析
【解析】
(1)设BC的解析式是y=ax+c,由直线AB:y=xb过A(6,0),可以求出b,因此可以求出B点的坐标,再由已知条件可求出C点的坐标,把B,C点的坐标分别代入求出a和c的值即可;
(2)过Q作QH⊥x轴于H,首先证明△BOP≌△PHQ,再分别证明△AHQ和△AOK为等腰直角三角形,问题得解.
(1)由已知:0=6b,
∴b=6,
∴AB:y=x+6.
∴B(0,6),
∴OB=6,
∵OB:OC=3:1,
OC=![]() =2,
=2,
∴C(2,0),
设BC的解析式是y=ax+c,代入得![]() ,
,
解得:![]() ,
,
∴直线BC的解析式是:y=3x+6;
(2)K点的位置不发生变化,K(0,6).
过Q作QH⊥x轴于H,
∵△BPQ是等腰直角三角形,
∴∠BPQ=90°,PB=PQ,
∵∠BOA=∠QHA=90°,
∴∠BPO=∠PQH,
∴△BOP≌△PHQ,
∴PH=BO,OP=QH,
∴PH+PO=BO+QH,
即OA+AH=BO+QH,
又OA=OB,
∴AH=QH,
∴△AHQ是等腰直角三角形,
∴∠QAH=45°,
∴∠OAK=45°,
∴△AOK为等腰直角三角形,
∴OK=OA=6,
∴K(0,6).

-
科目: 来源: 题型:
查看答案和解析>>【题目】学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子,碟子的个数与碟子的高度的关系如下表:
碟子的个数
碟子的高度(单位:cm)
1
2
2
2+1.5
3
2+3
4
2+4.5
…
…

(1)当桌子上放有x(个)碟子时,请写出此时碟子的高度(用含x的式子表示);
(2)分别从三个方向上看,其三视图如上图所示,厨房师傅想把它们整齐叠成一摞,求叠成一摞后的高度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂新开发生产一种机器,每台机器成本y(万元)与生产数量x(台)之间满足一次函数关系(其中10≤x≤70,且为整数),函数y与自变量x的部分对应值如表
 (单位:台)
(单位:台)10
20
30
 (单位:万元/台)
(单位:万元/台)60
55
50
(1)求y与x之间的函数关系式;

(2)市场调查发现,这种机器每月销售量z(台)与售价a(万元/台)之间满足如图所示的函数关系.则当该厂第一个月生产的这种机器40台都按同一售价全部售出,请求出该厂第一个月销售这种机器的总利润.(注:利润=售价﹣成本)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在射线AB上顺次取两点C,D,使AC=CD=1,以CD为边作矩形CDEF,DE=2,将射线AB绕点A沿逆时针方向旋转,旋转角记为α(其中0°<α<45°),旋转后记作射线AB′,射线AB′分别交矩形CDEF的边CF,DE于点G,H.若CG=x,EH=y,则下列函数图象中,能反映y与x之间关系的是( )

A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】王威调查统计了他们家3月份每次打电话的通话时长,并将统计结果进行分组(每组含最小值,不含最大值) ,将分组后的结果绘制成如图所示的频数分布直方图,则下列说法中不正确的是( )
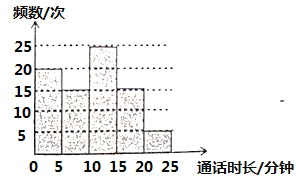
A.王威家3月份打电话的总频数为
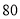 次
次B.王威家3月份每次打电话的通话时长在
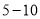 这组的频数为
这组的频数为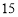 次
次C.王威家3月份每次打电话的通话时长在
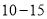 这组的频数最多
这组的频数最多D.王威家3月份每次打电话的通话时长在
 这组的频率为
这组的频率为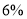
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中
 是原点,
是原点, 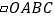 的顶点
的顶点  的坐标分别是
的坐标分别是 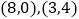 ,点
,点  把线段
把线段  三等分,延长
三等分,延长  分别交
分别交  于点
于点  ,连接
,连接  ,则下列结论:
,则下列结论:
① 是
是  的中点;②
的中点;②  与
与 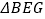 相似;③四边形
相似;③四边形  的面积是
的面积是  ;④
;④  ;其中正确的结论是 . (填写所有正确结论的序号)
;其中正确的结论是 . (填写所有正确结论的序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知平面直角坐标系中有一点

 点
点 到
到 轴的距离为
轴的距离为 时,求出点
时,求出点 的坐标;
的坐标; 点
点 的坐标为
的坐标为 ,且
,且 轴,求出点
轴,求出点 的坐标.
的坐标.
相关试题

