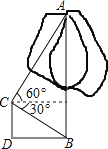
【题目】为申办2013年冬奥会,须改变某城市的交通状况,在街道拓宽工程中,要伐掉一棵树AB,在地面上事先划定以B为圆心,半径与AB等长的圆形危险区.现在某工人站在离B点3米远的D处,从C点测得树的顶端A点的仰角为60°,树的底部B点的俯角为30°.问:距离B点8米元的保护物是否存在危险?
参考答案:
【答案】距离B点8米远的保护物不在危险区内
【解析】
试题分析:首先根据题意分析图形;本题涉及到两个直角三角形,分别求解可得AB的值,比较AB与8的大小,进而可判断出答案.
解:作CE⊥AB于点D,
∴CE=BD=3,
在Rt△AEC中,AE=tan∠ACECE=tan60°×3=3![]() ,
,
在Rt△CEB中,BE=tan∠BCECE=tan30°×3=![]() ,
,
∴AB=AE+BE=3![]() +
+![]() =4
=4![]() ,
,
∵8>4![]() ,
,
∴距离B点8米远的保护物不在危险区内.
答:距离B点8米远的保护物不在危险区内.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. 有一组邻边相等的四边形是菱形
B. 有一个角是直角的菱形是正方形
C. 对角线相等的四边形是矩形
D. 一组对边平行,另一组对边相等的四边形是平行四边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上把数2对应的点移动3个单位后所得的对应点表示的数是( )
A. 5 B. ﹣1 C. 5或﹣1 D. 不确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个矩形的长比宽多1cm,面积是132cm2,则矩形的长为________cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,
中,  为
为 中点,
中点, 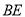 、
、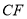 与射线
与射线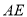 分别相交于点
分别相交于点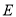 、
、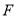 (射线
(射线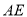 不经过点
不经过点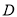 ).
).(1)如图①,当BE∥CF时,连接ED并延长交CF于点H. 求证:四边形BECH是平行四形;
(2)如图②,当BE⊥AE于点E,CF⊥AE于点F时,分别取AB、AC的中点M、N,连接ME、MD、NF、ND. 求证:AM=AN
(3)如图②,当BE⊥AE于点E,CF⊥AE于点F时,分别取AB、AC的中点M、N,连接ME、MD、NF、ND. 求证:∠EMD=∠FND.
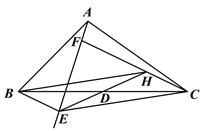
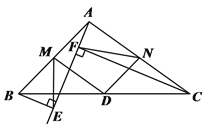
图① 图②
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,结论错误的是( )
A. 直径相等的两个圆是等圆
B. 长度相等的两条弧是等弧
C. 圆中最长的弦是直径
D. 一条弦把圆分成两条弧,这两条弧可能是等弧
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校开展以“倡导绿色出行,关爱师生健康”为主题的教育活动.为了了解本校师生的出行方式,在本校范围内随机抽查了部分师生,将收集的数据绘制成下列不完整的两种统计图.

请根据统计图提供的信息,解答下列问题:
(1)m= ;
(2)已知随机抽查的教师人数为学生人数的一半,请根据上述信息补全条形统计图,并标明相应数据;
(3)若全校师生共1800人,请你通过计算估计,全校师生乘私家车出行的有多少人?
相关试题

