【题目】在![]() 中,
中, ![]() 为
为![]() 中点,
中点, ![]() 、
、![]() 与射线
与射线![]() 分别相交于点
分别相交于点![]() 、
、![]() (射线
(射线![]() 不经过点
不经过点![]() ).
).
(1)如图①,当BE∥CF时,连接ED并延长交CF于点H. 求证:四边形BECH是平行四形;
(2)如图②,当BE⊥AE于点E,CF⊥AE于点F时,分别取AB、AC的中点M、N,连接ME、MD、NF、ND. 求证:AM=AN
(3)如图②,当BE⊥AE于点E,CF⊥AE于点F时,分别取AB、AC的中点M、N,连接ME、MD、NF、ND. 求证:∠EMD=∠FND.
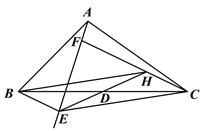
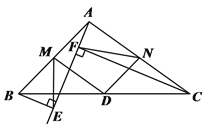
图① 图②
参考答案:
【答案】(1)证明见解析;(2)证明见解析;(3)证明见解析
【解析】试题分析:(1)根据两直线平行内错角相等求得∠DBE=∠DCH,然后依据AAS求得△BDE≌△CDH得出ED=HD,最后根据有一组对边平行且相等的四边形是平行四边形求得.
(2)连接FD、ED,延长ED交CF于点H,根据直角三角形斜边的中线定理和三角形的中位线定理求得ME=DN,MD=NF,从而证得AM=AN;
(3)在(2)的条件下根据SSS即可证明△MED≌△NDF,最后根据全等三角形的对应角相等求得∠EMD=∠FND.
试题解析:
(1)如图①,
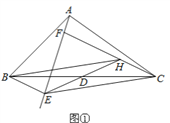
∵D为BC的中点,
∴BD=CD,
∵BE∥CF,
∴∠DBE=∠DCH,
在△BDE与△CDH中,
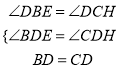 ,
,
∴△BDE≌△CDH(AAS),
∴ED=HD,
∴四边形BECH是平行四边形;
(2)如图②连接FD、ED,延长ED交CF于点H,
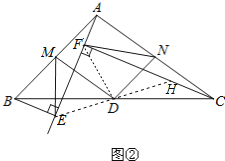
∵BE⊥AE,CF⊥AE,
∴BE∥CF,
由(1)可知△BDE≌△CDH,
∴DE=DH,
∴在Rt△EHF中,FD=DE=DH.
∵M为AB的中点,
∴在Rt△AEB中,ME=BM=AM,
同理,在Rt△ACF中,FN=AN=CN.
∵M、N、D分别为AB、AC、BC的中点,
∴![]()
![]()
![]()
(3)由上可知ME=DN,MD=NF,
在△MED与△NDF中,
 ,
,
∴△MED≌△NDF(SSS),
∴∠EMD=∠FND.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上把数2对应的点移动3个单位后所得的对应点表示的数是( )
A. 5 B. ﹣1 C. 5或﹣1 D. 不确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个矩形的长比宽多1cm,面积是132cm2,则矩形的长为________cm.
-
科目: 来源: 题型:
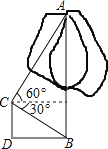
查看答案和解析>>【题目】为申办2013年冬奥会,须改变某城市的交通状况,在街道拓宽工程中,要伐掉一棵树AB,在地面上事先划定以B为圆心,半径与AB等长的圆形危险区.现在某工人站在离B点3米远的D处,从C点测得树的顶端A点的仰角为60°,树的底部B点的俯角为30°.问:距离B点8米元的保护物是否存在危险?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,结论错误的是( )
A. 直径相等的两个圆是等圆
B. 长度相等的两条弧是等弧
C. 圆中最长的弦是直径
D. 一条弦把圆分成两条弧,这两条弧可能是等弧
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校开展以“倡导绿色出行,关爱师生健康”为主题的教育活动.为了了解本校师生的出行方式,在本校范围内随机抽查了部分师生,将收集的数据绘制成下列不完整的两种统计图.

请根据统计图提供的信息,解答下列问题:
(1)m= ;
(2)已知随机抽查的教师人数为学生人数的一半,请根据上述信息补全条形统计图,并标明相应数据;
(3)若全校师生共1800人,请你通过计算估计,全校师生乘私家车出行的有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】研究发现,银原子的半径约是 0.00015 微米,把 0.00015 这个数字用 科学计数法表示应是( )
A. 1.5×10﹣4 B. 1.5×10﹣5 C. 15×10﹣5 D. 15×10﹣6
相关试题

