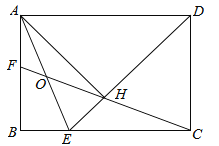
【题目】(3分)如图,在矩形ABCD中,BC=![]() AB,∠ADC的平分线交边BC于点E,AH⊥DE于点H,连接CH并延长交边AB于点F,连接AE交CF于点O.给出下列命题:
AB,∠ADC的平分线交边BC于点E,AH⊥DE于点H,连接CH并延长交边AB于点F,连接AE交CF于点O.给出下列命题:
①∠AEB=∠AEH;②DH=![]() EH;③HO=
EH;③HO=![]() AE;④BC﹣BF=
AE;④BC﹣BF=![]() EH.
EH.
其中正确命题的序号是 (填上所有正确命题的序号).
参考答案:
【答案】①③.
【解析】
试题在矩形ABCD中,AD=BC=![]() AB=
AB=![]() CD,∵DE平分∠ADC,∴∠ADE=∠CDE=45°,∵AD⊥DE,∴△ADH是等腰直角三角形,∴AD=
CD,∵DE平分∠ADC,∴∠ADE=∠CDE=45°,∵AD⊥DE,∴△ADH是等腰直角三角形,∴AD=![]() AB,∴AH=AB=CD,∵△DEC是等腰直角三角形,∴DE=
AB,∴AH=AB=CD,∵△DEC是等腰直角三角形,∴DE=![]() CD,∴AD=DE,∴∠AED=67.5°,∴∠AEB=180°﹣45°﹣67.5°=67.5°,∴∠AED=∠AEB,故①正确;
CD,∴AD=DE,∴∠AED=67.5°,∴∠AEB=180°﹣45°﹣67.5°=67.5°,∴∠AED=∠AEB,故①正确;
设DH=1,则AH=DH=1,AD=DE=![]() ,∴HE=
,∴HE=![]() ,∴
,∴![]() HE=
HE=![]() ,故②错误;
,故②错误;
∵∠AEH=67.5°,∴∠EAH=22.5°,∵DH=CH,∠EDC=45°,∴∠DHC=67.5°,∴∠OHA=22.5°,∴∠OAH=∠OHA,∴OA=OH,∴∠AEH=∠OHE=67.5°,∴OH=OE,∴OH=![]() AE,故③正确;
AE,故③正确;
∵AH=DH,CD=CE,在△AFH与△CHE中,∵∠AHF=∠HCE=22.5°,∠FAH=∠HEC=45°,AH=CE,∴△AFH≌△CHE,∴AF=EH,在△ABE与△AHE中,∵AB=AH,∠BEA=∠HEA,AE=AE,∴△ABE≌△AHE,∴BE=EH,∴BC﹣BF=(BE+CE)﹣(AB=AF)=(CD+EH)﹣(CD﹣EH)=2EH,故④错误,故答案为:①③.
-
科目: 来源: 题型:
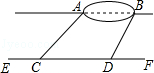
查看答案和解析>>【题目】小宇想测量位于池塘两端的A、B两点的距离.他沿着与直线AB平行的道路EF行走,当行走到点C处,测得∠ACF=45°,再向前行走100米到点D处,测得∠BDF=60°.若直线AB与EF之间的距离为60米,求A、B两点的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列做法正确的是( )
A. 由2(x+1)=x+7去括号、移项、合并同类项,得x=5
B. 由
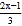 =1+
=1+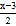 去分母,得2(2x﹣1)=1+3(x﹣3)
去分母,得2(2x﹣1)=1+3(x﹣3)C. 由2(2x﹣1)﹣3(x﹣3)=1去括号,得4x﹣2﹣3x﹣9=1
D. 由7x=4x﹣3移项,得7x﹣4x=3
-
科目: 来源: 题型:
查看答案和解析>>【题目】在等边△ABC中,以BC为直径的⊙O与AB交于点D,DE⊥AC,垂足为点E.

(1)求证:DE为⊙O的切线;
(2)计算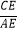 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
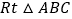 中,
中,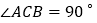 ,点O是BC上一点,以点O圆心,OC为半径的圆交BC于点D,恰好与AB相切于点E.
,点O是BC上一点,以点O圆心,OC为半径的圆交BC于点D,恰好与AB相切于点E.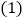 求证:AO是
求证:AO是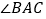 的平分线;
的平分线;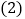 若
若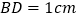 ,
,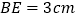 ,求
,求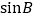 及AC的长.
及AC的长.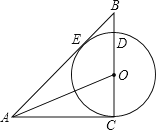
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某工艺品厂生产一款工艺品、已知这款工艺品的生产成本为每件60元. 经市场调研发现:该款工艺品每天的销售量y(件)与售价x(元)之间存在着如下表所示的一次函数关系.
售价x(元)
…
70
90
…
销售量y(件)
…
3000
1000
…
(利润=(售价﹣成本价)×销售量)
(1)求销售量y(件)与售价x(元)之间的函数关系式;
(2)你认为如何定价才能使工艺品厂每天获得的利润为40000元? -
科目: 来源: 题型:
查看答案和解析>>【题目】猜想与证明:
如图1,摆放矩形纸片ABCD与矩形纸片ECGF,使B、C、G三点在一条直线上,CE在边CD上,连接AF,若M为AF的中点,连接DM、ME,试猜想DM与ME的关系,并证明你的结论.
拓展与延伸: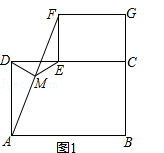
(1)若将”猜想与证明“中的纸片换成正方形纸片ABCD与正方形纸片ECGF,其他条件不变,则DM和ME的关系为 .
(2)如图2摆放正方形纸片ABCD与正方形纸片ECGF,使点F在边CD上,点M仍为AF的中点,试证明(1)中的结论仍然成立.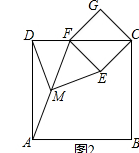
相关试题

