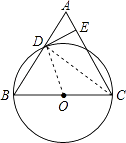
【题目】在等边△ABC中,以BC为直径的⊙O与AB交于点D,DE⊥AC,垂足为点E. 
(1)求证:DE为⊙O的切线;
(2)计算 ![]() .
.
参考答案:
【答案】
(1)证明:连接OD,
∵△ABC为等边三角形,
∴∠ABC=60°,
又∵OD=OB,
∴△OBD为等边三角形,
∴∠BOD=60°=∠ACB,
∴OD∥AC,
又∵DE⊥AC,
∴∠ODE=∠AED=90°,
∴DE为⊙O的切线
(2)解:连接CD,
∵BC为⊙O的直径,
∴∠BDC=90°,
又∵△ABC为等边三角形,
∴AD=BD= ![]() AB,
AB,
在Rt△AED中,∠A=60°,
∴∠ADE=30°,
∴AE= ![]() AD=
AD= ![]() AC,CE=AC﹣AE=
AC,CE=AC﹣AE= ![]() AC,
AC,
∴ ![]() =3.
=3.
【解析】(1)连接OD,根据等边三角形性质得出∠B=∠A=60°,求出等边三角形BDO,求出∠BDO,∠A,推出OD∥AC,推出OD⊥DE,根据切线的判定推出即可;(2)求出AD= ![]() AC,求出AE=
AC,求出AE= ![]() AC,CE=
AC,CE= ![]() AC,即可求出答案.
AC,即可求出答案.
【考点精析】本题主要考查了平行线的判定和等边三角形的性质的相关知识点,需要掌握同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行;等边三角形的三个角都相等并且每个角都是60°才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解学生体育训练的情况,某市从全市九年级学生中随机抽取部分学生进行了一次体育科目测试(把成绩结果分为四个等级:A级:优秀;B级:良好;C级:及格;D级:不及格),并将测试结果绘成了如下两幅不完整的统计图.请根据统计图中的信息解答下列问题:
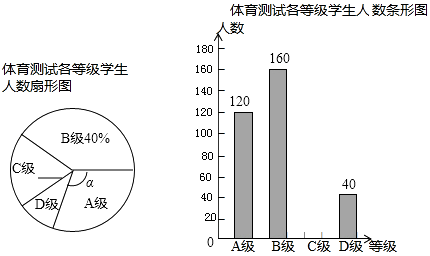
(1)求本次抽样测试的学生人数;
(2)求扇形图中∠α的度数,并把条形统计图补充完整;
(3)该市九年级共有学生9000名,如果全部参加这次体育测试,则测试等级为D的约有多少人? -
科目: 来源: 题型:
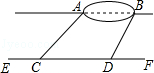
查看答案和解析>>【题目】小宇想测量位于池塘两端的A、B两点的距离.他沿着与直线AB平行的道路EF行走,当行走到点C处,测得∠ACF=45°,再向前行走100米到点D处,测得∠BDF=60°.若直线AB与EF之间的距离为60米,求A、B两点的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列做法正确的是( )
A. 由2(x+1)=x+7去括号、移项、合并同类项,得x=5
B. 由
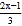 =1+
=1+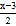 去分母,得2(2x﹣1)=1+3(x﹣3)
去分母,得2(2x﹣1)=1+3(x﹣3)C. 由2(2x﹣1)﹣3(x﹣3)=1去括号,得4x﹣2﹣3x﹣9=1
D. 由7x=4x﹣3移项,得7x﹣4x=3
-
科目: 来源: 题型:
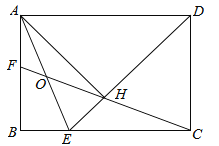
查看答案和解析>>【题目】(3分)如图,在矩形ABCD中,BC=
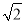 AB,∠ADC的平分线交边BC于点E,AH⊥DE于点H,连接CH并延长交边AB于点F,连接AE交CF于点O.给出下列命题:
AB,∠ADC的平分线交边BC于点E,AH⊥DE于点H,连接CH并延长交边AB于点F,连接AE交CF于点O.给出下列命题:①∠AEB=∠AEH;②DH=
 EH;③HO=
EH;③HO= AE;④BC﹣BF=
AE;④BC﹣BF=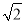 EH.
EH.其中正确命题的序号是 (填上所有正确命题的序号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
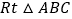 中,
中,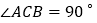 ,点O是BC上一点,以点O圆心,OC为半径的圆交BC于点D,恰好与AB相切于点E.
,点O是BC上一点,以点O圆心,OC为半径的圆交BC于点D,恰好与AB相切于点E. 求证:AO是
求证:AO是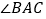 的平分线;
的平分线;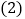 若
若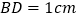 ,
,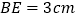 ,求
,求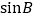 及AC的长.
及AC的长.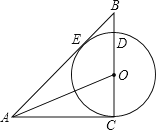
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某工艺品厂生产一款工艺品、已知这款工艺品的生产成本为每件60元. 经市场调研发现:该款工艺品每天的销售量y(件)与售价x(元)之间存在着如下表所示的一次函数关系.
售价x(元)
…
70
90
…
销售量y(件)
…
3000
1000
…
(利润=(售价﹣成本价)×销售量)
(1)求销售量y(件)与售价x(元)之间的函数关系式;
(2)你认为如何定价才能使工艺品厂每天获得的利润为40000元?
相关试题

