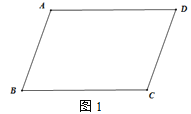
【题目】如图1,已知AD∥BC,∠B=∠D.
(1)求证:AB∥CD;
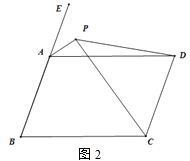
(2)如图2,点E为BA延长线上一点,∠EAD与∠BCD的角平分线交于点P.
①求∠APC的度数;
②连接DP,若∠PDC=750,则∠DPC-![]() ∠B=________.
∠B=________.
参考答案:
【答案】90°
【解析】
(1)根据平行线的性质和判定结合已知条件进行分析证明即可;
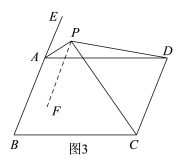
(2)①如图3,过点P作PF∥AB,结合已知条件易得∠EAP=∠APF,∠DCP=∠CPF,从而可得∠APC=∠EAP+∠DCP,由已知易得∠EAD=∠B,∠B+∠BCD=180°,进而可得∠EAD+∠BCD=180°,结合AP平分∠EAD,CP平分∠BCD即可得到∠APC=∠EAP+∠DCP=90°;②如图4,延长DP交BA的延长线于点M,由已知易得I、∠MPA+∠APF=75°,由∠APC=90°可得II、∠MPA+∠DPC=90°,再证∠APF=![]() ∠B,即可由I-II得到所求结果.
∠B,即可由I-II得到所求结果.
(1)∵AD∥BC,
∴∠ A+∠ B=180°,
∵∠ B=∠ D,即∠ A+∠ D =180°,
∴ AB∥CD;
(2)①过点P作直线PF∥AB,
∵在平行四边形ABCD中,AB∥CD,AD∥BC,
∴∠EAD=∠B,∠B+∠BCD=180°,AB∥PF∥CD,
∴∠EAD+∠BCD=180°,
∵AP平分∠EAD,CP平分∠BCD,
∴∠EAP=![]() ∠EAD,∠DCP=
∠EAD,∠DCP=![]() ∠BCD,
∠BCD,
∴∠EAP+∠DCP=![]() (∠EAD+∠BCD)=90°,
(∠EAD+∠BCD)=90°,
∵AB∥PF∥CD,
∴∠APF=∠EAP,∠CPF=∠DCP,
∴∠APC=∠APF+∠CPF=∠EAP+∠DCP=90°,即∠APC=90°;
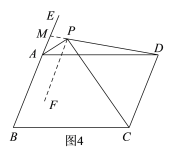
②如图4,延长DP交BA的延长线于点M,
∵AB∥PF∥CD,
∴∠APF=∠EAP=![]() ∠EAD=
∠EAD=![]() ∠B,∠MPA+∠APF=∠MPF=∠PDC=75°,
∠B,∠MPA+∠APF=∠MPF=∠PDC=75°,
∵∠APC=90°,
∴∠MPA+∠DPC=90°,
∴(∠MPA+∠DPC)-(∠MPA+∠APF)=90°-75°=15°,
∴∠DPC-∠APF=15°,
∴∠DPC-![]() ∠B=15°.
∠B=15°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的口袋里装有红、黑、绿三种颜色的乒乓球(除颜色外其余都相同),其中红球有2个,黑球有1个,绿球有3个,第一次任意摸出一个球(不放回),第二次再摸出一个球,则两次摸到的都是红球的概率为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在圆心角为90°的扇形OAB中,半径OA=2cm,C为
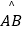 的中点,D、E分别是OA、OB的中点,则图中阴影部分的面积为cm2 .
的中点,D、E分别是OA、OB的中点,则图中阴影部分的面积为cm2 . 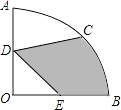
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个矩形纸片OACB,将该纸片放置在平面直角坐标系中,点A(11,0),点B(0,6),点P为BC边上的动点(点P不与点B,C重合),经过点O、P折叠该纸片,得点B′和折痕OP(如图①)经过点P再次折叠纸片,使点C落在直线PB′上,得点C′和折痕PQ(如图②),当点C′恰好落在OA上时,点P的坐标是 .
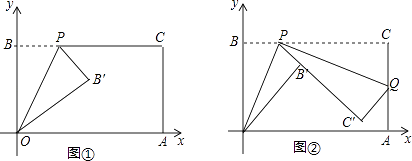
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BAC=90°,∠C=30°,以边上AC上一点O为圆心,OA为半径作⊙O,⊙O恰好经过边BC的中点D,并与边AC相交于另一点F.

(1)求证:BD是⊙O的切线.
(2)若AB= ,E是半圆
,E是半圆  上一动点,连接AE,AD,DE. 填空:
上一动点,连接AE,AD,DE. 填空:
①当 的长度是时,四边形ABDE是菱形;
的长度是时,四边形ABDE是菱形;
②当 的长度是时,△ADE是直角三角形.
的长度是时,△ADE是直角三角形. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,在平面直角坐标系中,A(1,a)、B(b,1),其中a、b满足
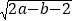 +(a+b-7)2=0.
+(a+b-7)2=0.(1) 求a、b的值;
(2) 平移线段AB至CD,其中A、B的对应点分别为C、D,若D的坐标为(0,n)且n<0,若四边形ABDC的面积为20,求D的坐标;
(3)在(2)的条件下,将线段AB绕点A以每秒80的速度顺时针旋转,同时线段CD绕点D以每秒20的速度顺时针旋转(当AB旋转到一周时两线段同时停止旋转),设运动时间为t秒,当t为何值时,直线AB与直线CD的夹角为600?请说明理由.
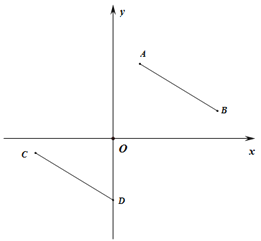
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在五边形 ABCDE 中,∠A+∠B+∠E=α,DP,CP 分别平分∠EDC,∠BCD,则∠P 的度数是( )

A. 90°+
 α B.
α B.  α﹣90° C.
α﹣90° C.  α D. 540° -
α D. 540° - α
α
相关试题

