【题目】如图,在五边形 ABCDE 中,∠A+∠B+∠E=α,DP,CP 分别平分∠EDC,∠BCD,则∠P 的度数是( )

A. 90°+![]() α B.
α B. ![]() α﹣90° C.
α﹣90° C. ![]() α D. 540° -
α D. 540° -![]() α
α
参考答案:
【答案】B
【解析】根据五边形的内角和等于540°,由∠A+∠B+∠E=α,可求∠BCD+∠CDE的度数,再根据角平分线的定义可得∠PDC与∠PCD的角度和,进一步求得∠P的度数.
∵五边形的内角和等于540°,∠A+∠B+∠E=α,
∴∠BCD+∠CDE=540°-α,
∵∠BCD、∠CDE的平分线在五边形内相交于点O,
∴∠PDC+∠PCD=![]() (∠BCD+∠CDE)=270°-
(∠BCD+∠CDE)=270°-![]() α,
α,
∴∠P=180°-(270°-![]() α)=
α)=![]() α-90°,
α-90°,
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知AD∥BC,∠B=∠D.
(1)求证:AB∥CD;
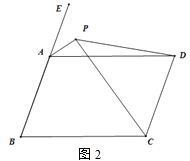
(2)如图2,点E为BA延长线上一点,∠EAD与∠BCD的角平分线交于点P.
①求∠APC的度数;
②连接DP,若∠PDC=750,则∠DPC-
 ∠B=________.
∠B=________.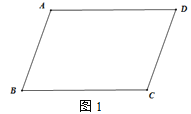
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BAC=90°,∠C=30°,以边上AC上一点O为圆心,OA为半径作⊙O,⊙O恰好经过边BC的中点D,并与边AC相交于另一点F.

(1)求证:BD是⊙O的切线.
(2)若AB= ,E是半圆
,E是半圆  上一动点,连接AE,AD,DE. 填空:
上一动点,连接AE,AD,DE. 填空:
①当 的长度是时,四边形ABDE是菱形;
的长度是时,四边形ABDE是菱形;
②当 的长度是时,△ADE是直角三角形.
的长度是时,△ADE是直角三角形. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,在平面直角坐标系中,A(1,a)、B(b,1),其中a、b满足
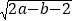 +(a+b-7)2=0.
+(a+b-7)2=0.(1) 求a、b的值;
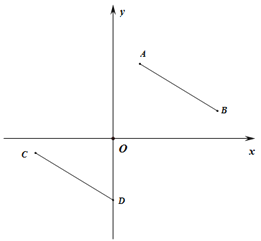
(2) 平移线段AB至CD,其中A、B的对应点分别为C、D,若D的坐标为(0,n)且n<0,若四边形ABDC的面积为20,求D的坐标;
(3)在(2)的条件下,将线段AB绕点A以每秒80的速度顺时针旋转,同时线段CD绕点D以每秒20的速度顺时针旋转(当AB旋转到一周时两线段同时停止旋转),设运动时间为t秒,当t为何值时,直线AB与直线CD的夹角为600?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在“爱我中华”中学生演讲比赛中,五位评委分别给甲、乙两位选手的评分如下:甲:8,7,9,8,8;乙:7,9,6,9,9,则下列说法中错误的是( )
A. 甲、乙得分的平均数都是8 B. 甲得分的众数是8,乙得分的众数是9
C. 甲得分的中位数是9,乙得分的中位数是6 D. 甲得分的方差比乙得分的方差小
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB∥CD,F为CD上一点,∠EFD=60°,∠AEC=2∠CEF,若6°<∠BAE<15°,∠C的度数为整数,则∠C的度数为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】当今社会手机越来越普及,有很多人开始过份依赖手机,一天中使用手机时间过长而形成了“手机瘾”.为了解我校初三年级学生的手机使用情况,学生会随机调查了部分学生的手机使用时间,将调查结果分成五类:A、基本不用;B、平均一天使用1~2小时;C、平均一天使用2~4小时;D、平均一天使用4~6小时;E、平均一天使用超过6小时.并用得到的数据绘制成了如下两幅不完整的统计图(图1、2),请根据相关信息,解答下列问题:
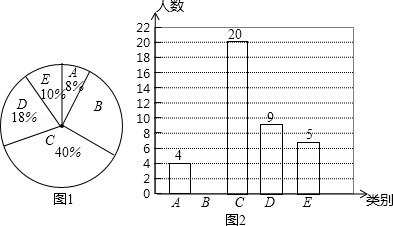
(1)将上面的条形统计图补充完整;
(2)若一天中手机使用时间超过6小时,则患有严重的“手机瘾”.我校初三年级共有1490人,试估计我校初三年级中约有多少人患有严重的“手机瘾”;
(3)在被调查的基本不用手机的4位同学中有2男2女,现要从中随机再抽两名同学去参加座谈,请你用列表法或树状图方法求出所选两位同学恰好是一名男同学和一位女同学的概率.
相关试题

