【题目】在四边形ABCD中,对角线AC与BD交于点O,E是OC上任意一点,AG⊥BE于点G,交直线BD于点F.

(1)如图1,若四边形ABCD是正方形,判断AF与BE的数量关系:AF与BE的数量关系是 ;
(2)如图2,若四边形ABCD是菱形,∠ABC=120°,求![]() 的值;
的值;
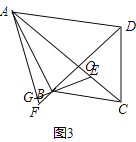
(3)如图3,若四边形ABCD中,AC⊥BD,∠ABC=α,∠DBC=β,请你补全图形,并直接写出:![]() = (用含α,β的式子表示).
= (用含α,β的式子表示).
参考答案:
【答案】(1)AF=BE(2)![]() (3)tan(α﹣β)
(3)tan(α﹣β)
【解析】
试题分析:(1)根据正方形的性质和全等三角形的性质即可得到结论;
(2)根据四边形ABCD是菱形和∠ABC=120°,推出AC⊥BD,∠ABO=60°,根据余角的性质得到∠AFO=∠BEA,又因为∠AOF=∠BOE=90°,推出三角形相似,即可得到结论;
(3)根据垂直的定义得到∠AGB=∠AOB=90°,推出A,G,B,O四点共圆,根据圆内接四边形的性质得到∠GAO=∠GAO,推出△AOF∽△BOE,即可得到结论.
解:(1)AF=BE;
∵四边形ABCD是正方形,
∴∠AOB=∠BOC=90°,AO=BO,
∵AG⊥BE,∠AFO=∠BFG,
∴∠FAO=∠FBG,
在△AFO与△BFO中,
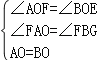 ,
,
∴△AFO≌△BFO,
∴AF=BE;
故答案为:AF=BE;
(2)∵四边形ABCD是菱形,∠ABC=120°,
∴AC⊥BD,∠ABO=60°,
∴∠FAO+∠AFO=90°,
∵AG⊥BE,
∴∠EAG+∠BEA=90°,
∴∠AFO=∠BEA,
又∵∠AOF=∠BOE=90°,
∴△AOF∽△BOE,
∴![]() =
=![]() ,
,
∵∠ABO=60°,AC⊥BD,
∴![]() =tan60°=
=tan60°=![]() ,
,
∴![]() =
=![]() ;
;
(3)如图3,∵AG⊥BE,AC⊥BD,
∴∠AGB=∠AOB=90°,
∴A,G,B,O四点共圆,
∴∠GAO=∠GAO,
∴∠AOF=∠BOE=90°,
∴△AOF∽△BOE,
∴![]() =
=![]() ,
,
∵∠ABO=∠ABC﹣∠OBC=α﹣β,AC⊥BD,
∴![]() =tan(α﹣β),
=tan(α﹣β),
∴![]() =tan(α﹣β).
=tan(α﹣β).
故答案为:tan(α﹣β).
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x-y=3且xy=1,则代数式(1+x)(y-1)的值等于( )
A. -3 B. 3 C. -1 D. -5
-
科目: 来源: 题型:
查看答案和解析>>【题目】你对“0”有多少了解?下列关于“0”的说法错误的是( )
A. 任何数与0相乘都得0 B. 0是最小的有理数
C. 绝对值最小的有理数是0 D. 0没有倒数
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有足够多的边长为a的小正方形(A类)、长为a宽为b的长方形(B类)以及边长为b的大正方形(C类),发现利用图①中的三种材料各若干可以拼出一些长方形来解释某些等式. 比如图②可以解释为:(a+2b)(a+b)=a2+3ab+2b2
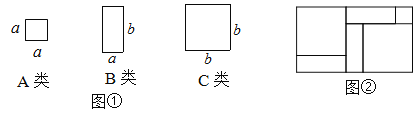

(1)取图①中的若干个(三种图形都要取到)拼成一个长方形,使它的边长分别为(2a+b)、(a+2b),不画图形,试通过计算说明需要C类卡片多少张;
(2)若取其中的若干个(三种图形都要取到)拼成一个长方形,使它的面积等于a2+5ab+4b2,画出这个长方形,并根据图形对多项式a2+5ab+4b2进行因式分解;
(3) 如图③,大正方形的边长为m,小正方形的边长为n,若用x、y表示四个矩形的两边长(x>y),观察图案并判断,将正确关系式的序号填写在横线上______ _____(填写序号)
①.xy =
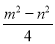 ②.x+y=m ③.x2-y2=m·n ④.x2+y2 =
②.x+y=m ③.x2-y2=m·n ④.x2+y2 =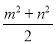
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知P(﹣3,m)和 Q(1,m)是抛物线y=x2+bx﹣3上的两点.

(1)求b的值;
(2)将抛物线y=x2+bx﹣3的图象向上平移k(是正整数)个单位,使平移后的图象与x轴无交点,求k的最小值;
(3)将抛物线y=x2+bx﹣3的图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,得到一个新的图象,请你结合新图象回答:当直线y=x+n与这个新图象有两个公共点时,求n的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设p、q都是实数,且p<q.我们规定:满足不等式p≤x≤q的实数x的所有取值的全体叫做闭区间,表示为[p,q].对于一个函数,如果它的自变量x与函数值y满足:当p≤x≤q时,有p≤y≤q,我们就称此函数是闭区间[p,q]上的“闭函数”.
(1)反比例函数y=
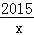 是闭区间[1,2015]上的“闭函数”吗?请判断并说明理由.
是闭区间[1,2015]上的“闭函数”吗?请判断并说明理由.(2)若一次函数y=kx+b(k≠0)是闭区间[m,n]上的“闭函数”,求此一次函数的解析式;
(3)若实数c,d满足c<d,且d>2,当二次函数y=
 x2﹣2x是闭区间[c,d]上的“闭函数”时,求c,d的值.
x2﹣2x是闭区间[c,d]上的“闭函数”时,求c,d的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】正比例函数y=x与反比例函数y=
 的图象相交于A、C两点.AB⊥x轴于B,CD⊥x轴于D(如图),则四边形ABCD的面积为( )
的图象相交于A、C两点.AB⊥x轴于B,CD⊥x轴于D(如图),则四边形ABCD的面积为( )
A.1 B.
 C.2 D.
C.2 D.
相关试题

