【题目】设p、q都是实数,且p<q.我们规定:满足不等式p≤x≤q的实数x的所有取值的全体叫做闭区间,表示为[p,q].对于一个函数,如果它的自变量x与函数值y满足:当p≤x≤q时,有p≤y≤q,我们就称此函数是闭区间[p,q]上的“闭函数”.
(1)反比例函数y=![]() 是闭区间[1,2015]上的“闭函数”吗?请判断并说明理由.
是闭区间[1,2015]上的“闭函数”吗?请判断并说明理由.
(2)若一次函数y=kx+b(k≠0)是闭区间[m,n]上的“闭函数”,求此一次函数的解析式;
(3)若实数c,d满足c<d,且d>2,当二次函数y=![]() x2﹣2x是闭区间[c,d]上的“闭函数”时,求c,d的值.
x2﹣2x是闭区间[c,d]上的“闭函数”时,求c,d的值.
参考答案:
【答案】(1)是闭区间上[1,2014]的“闭函数”,理由见解析(2)y=x或y=﹣x+m+n(3)c=﹣2,d=6为所求的实数
【解析】
试题分析:(1)根据反比例函数y=![]() 的单调区间进行判断;
的单调区间进行判断;
(2)根据新定义运算法则列出关于系数k、b的方程组,通过解该方程组即可求得系数k、b的值;
(3)y=![]() x2﹣2x=
x2﹣2x=![]() (x2﹣4x+4)﹣2=
(x2﹣4x+4)﹣2=![]() (x﹣2)2﹣2,所以该二次函数的图象开口方向向上,最小值是﹣2,且当x<2时,y随x的增大而减小;当x>2时,y随x的增大而增大.由于c<d,且d>2,所以分两种情况进行讨论:①c<2<d;②c≥2.
(x﹣2)2﹣2,所以该二次函数的图象开口方向向上,最小值是﹣2,且当x<2时,y随x的增大而减小;当x>2时,y随x的增大而增大.由于c<d,且d>2,所以分两种情况进行讨论:①c<2<d;②c≥2.
解:(1)是由函数y=![]() 的图象可知,
的图象可知,
当1≤x≤2015时,函数值y随着自变量x的增大而减小.
而当x=1时,y=2015;
x=2015,y=1,
故也有1≤y≤2015,
所以,函数y=![]() 是闭区间上[1,2014]的“闭函数”
是闭区间上[1,2014]的“闭函数”
(2)因为一次函数y=kx+b(k≠0)是闭区间[m,n]上的“闭函数”,
所以根据一次函数的图象与性质,
必有:①当k>0时,![]() (m≠n)
(m≠n)
解得k=1,b=0,
∴一次函数的解析式为y=x.
②当k<0时,![]() (m≠n),
(m≠n),
解得k=﹣1,b=m+n
∴一次函数的解析式为y=﹣x+m+n故一次函数的解析式为y=x或y=﹣x+m+n
(3)由于函数y=![]() x2﹣2x的图象开口向上,且对称轴为x=2,顶点为(2,﹣2)
x2﹣2x的图象开口向上,且对称轴为x=2,顶点为(2,﹣2)
由题意根据图象,分以下两种情况讨论:
①当2≤c<d时,必有x=c,时,y=c且x=d时,y=d即方程y=![]() x2﹣2x=x必有两个不等的实数根,解得x1=0,x2=6,而0,6分布在2的两边,这与2≤c<d矛盾,舍去;
x2﹣2x=x必有两个不等的实数根,解得x1=0,x2=6,而0,6分布在2的两边,这与2≤c<d矛盾,舍去;
②当c<2<d时,必有函数值y的最小值为﹣2,由于此二次函数是闭区间[c,d]上的“闭函数”,故必有c=﹣2,从而有[c,d]=[﹣2,d].
而当x=﹣2时,y=6即得点(﹣2,6),又点(﹣2,6)关于对称轴x=2的对称点为(6,6),由“闭函数”的定义可知必有x=d时,y=d,即![]() d2﹣2d=d,解得d1=0,d2=6,故可得c=﹣2,d=6符合题意,
d2﹣2d=d,解得d1=0,d2=6,故可得c=﹣2,d=6符合题意,
综上所述,c=﹣2,d=6为所求的实数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有足够多的边长为a的小正方形(A类)、长为a宽为b的长方形(B类)以及边长为b的大正方形(C类),发现利用图①中的三种材料各若干可以拼出一些长方形来解释某些等式. 比如图②可以解释为:(a+2b)(a+b)=a2+3ab+2b2
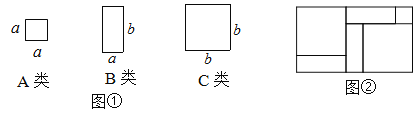

(1)取图①中的若干个(三种图形都要取到)拼成一个长方形,使它的边长分别为(2a+b)、(a+2b),不画图形,试通过计算说明需要C类卡片多少张;
(2)若取其中的若干个(三种图形都要取到)拼成一个长方形,使它的面积等于a2+5ab+4b2,画出这个长方形,并根据图形对多项式a2+5ab+4b2进行因式分解;
(3) 如图③,大正方形的边长为m,小正方形的边长为n,若用x、y表示四个矩形的两边长(x>y),观察图案并判断,将正确关系式的序号填写在横线上______ _____(填写序号)
①.xy =
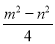 ②.x+y=m ③.x2-y2=m·n ④.x2+y2 =
②.x+y=m ③.x2-y2=m·n ④.x2+y2 =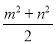
-
科目: 来源: 题型:
查看答案和解析>>【题目】在四边形ABCD中,对角线AC与BD交于点O,E是OC上任意一点,AG⊥BE于点G,交直线BD于点F.

(1)如图1,若四边形ABCD是正方形,判断AF与BE的数量关系:AF与BE的数量关系是 ;
(2)如图2,若四边形ABCD是菱形,∠ABC=120°,求
 的值;
的值;(3)如图3,若四边形ABCD中,AC⊥BD,∠ABC=α,∠DBC=β,请你补全图形,并直接写出:
 = (用含α,β的式子表示).
= (用含α,β的式子表示). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知P(﹣3,m)和 Q(1,m)是抛物线y=x2+bx﹣3上的两点.

(1)求b的值;
(2)将抛物线y=x2+bx﹣3的图象向上平移k(是正整数)个单位,使平移后的图象与x轴无交点,求k的最小值;
(3)将抛物线y=x2+bx﹣3的图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,得到一个新的图象,请你结合新图象回答:当直线y=x+n与这个新图象有两个公共点时,求n的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】正比例函数y=x与反比例函数y=
 的图象相交于A、C两点.AB⊥x轴于B,CD⊥x轴于D(如图),则四边形ABCD的面积为( )
的图象相交于A、C两点.AB⊥x轴于B,CD⊥x轴于D(如图),则四边形ABCD的面积为( )
A.1 B.
 C.2 D.
C.2 D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的三个函数图象中,有两个函数图象能近似地刻画如下a,b两个情境:
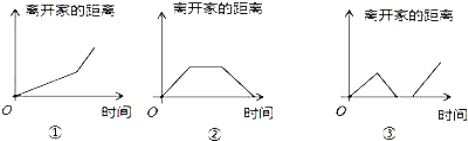
情境a:小芳离开家不久,发现把作业本忘在家里,于是返回了家里找到了作业本再去学校;
情境b:小芳从家出发,走了一段路程后,为了赶时间,以更快的速度前进.则情境a,b所对应的函数图象分别是( )
A. ③、② B. ②、③ C. ①、③ D. ③、①
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上标识4与-3的两个点之间的距离是( )
A. -1 B. 1 C. -7 D. 7
相关试题

