搜索
【题目】正比例函数y=x与反比例函数y=
的图象相交于A、C两点．AB⊥x轴于B，CD⊥x轴于D（如图），则四边形ABCD的面积为（ ）
A．1 B．
C．2 D．
参考答案：
【答案】C
【解析】
试题分析：首先根据反比例函数图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系即S=
|k|，得出S△AOB=S△ODC=，再根据反比例函数的对称性可知：OB=OD，得出S△AOB=S△ODA，S△ODC=S△OBC，最后根据四边形ABCD的面积=S△AOB+S△ODA+S△ODC+S△OBC，得出结果．
解：根据反比例函数的对称性可知：OB=OD，AB=CD，
∴四边形ABCD的面积=S△AOB+S△ODA+S△ODC+S△OBC=1×2=2．
故选C．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在四边形ABCD中，对角线AC与BD交于点O，E是OC上任意一点，AG⊥BE于点G，交直线BD于点F．
（1）如图1，若四边形ABCD是正方形，判断AF与BE的数量关系：AF与BE的数量关系是 ；
（2）如图2，若四边形ABCD是菱形，∠ABC=120°，求
的值；（3）如图3，若四边形ABCD中，AC⊥BD，∠ABC=α，∠DBC=β，请你补全图形，并直接写出：
= （用含α，β的式子表示）． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知P（﹣3，m）和 Q（1，m）是抛物线y=x2+bx﹣3上的两点．
（1）求b的值；
（2）将抛物线y=x2+bx﹣3的图象向上平移k（是正整数）个单位，使平移后的图象与x轴无交点，求k的最小值；
（3）将抛物线y=x2+bx﹣3的图象在x轴下方的部分沿x轴翻折，图象的其余部分保持不变，得到一个新的图象，请你结合新图象回答：当直线y=x+n与这个新图象有两个公共点时，求n的取值范围．
-
科目： 来源： 题型：
查看答案和解析>>【题目】设p、q都是实数，且p＜q．我们规定：满足不等式p≤x≤q的实数x的所有取值的全体叫做闭区间，表示为[p，q]．对于一个函数，如果它的自变量x与函数值y满足：当p≤x≤q时，有p≤y≤q，我们就称此函数是闭区间[p，q]上的“闭函数”．
（1）反比例函数y=
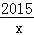是闭区间[1，2015]上的“闭函数”吗？请判断并说明理由．（2）若一次函数y=kx+b（k≠0）是闭区间[m，n]上的“闭函数”，求此一次函数的解析式；
（3）若实数c，d满足c＜d，且d＞2，当二次函数y=
x2﹣2x是闭区间[c，d]上的“闭函数”时，求c，d的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】在如图所示的三个函数图象中，有两个函数图象能近似地刻画如下a，b两个情境：
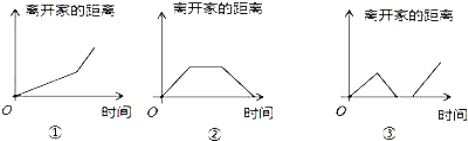
情境a：小芳离开家不久，发现把作业本忘在家里，于是返回了家里找到了作业本再去学校；
情境b：小芳从家出发，走了一段路程后，为了赶时间，以更快的速度前进．则情境a，b所对应的函数图象分别是（ ）
A. ③、② B. ②、③ C. ①、③ D. ③、①
-
科目： 来源： 题型：
查看答案和解析>>【题目】在数轴上标识4与-3的两个点之间的距离是（ ）
A. -1 B. 1 C. -7 D. 7
-
科目： 来源： 题型：
查看答案和解析>>【题目】命题“对顶角相等．”的逆命题是 命题（填“真”或“假”）．
相关试题
