【题目】如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y= ![]() (k>0,x>0)的图象上,点D的坐标为(
(k>0,x>0)的图象上,点D的坐标为( ![]() ,2).
,2).
(1)求k的值;
(2)若将菱形ABCD沿x轴正方向平移,当菱形的一个顶点恰好落在函数y= ![]() (k>0,x>0)的图象上时,求菱形ABCD平移的距离.
(k>0,x>0)的图象上时,求菱形ABCD平移的距离.
参考答案:
【答案】
(1)
解:作DE⊥BO,DF⊥x轴于点F,
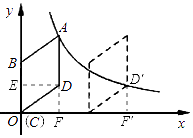
∵点D的坐标为( ![]() ,2),
,2),
∴DO=AD=3,
∴A点坐标为:( ![]() ,5),
,5),
∴k=5 ![]() ;
;
(2)
解:∵将菱形ABCD向右平移,使点D落在反比例函数y= ![]() (x>0)的图象上D′,
(x>0)的图象上D′,
∴DF=D′F′=2,
∴D′点的纵坐标为2,设点D′(x,2)
∴2= ![]() ,解得x=
,解得x= ![]() ,
,
∴FF′=OF′﹣OF= ![]() ﹣
﹣ ![]() =
= ![]() ,
,
∴菱形ABCD平移的距离为 ![]() ,
,
同理,将菱形ABCD向右平移,使点B落在反比例函数y= ![]() (x>0)的图象上,
(x>0)的图象上,
菱形ABCD平移的距离为 ![]() ,
,
综上,当菱形ABCD平移的距离为 ![]() 或
或 ![]() 时,菱形的一个顶点恰好落在函数图象上.
时,菱形的一个顶点恰好落在函数图象上.
【解析】(1)根据菱形的性质和D的坐标即可求出A的坐标,代入求出即可;(2)B和D可能落在反比例函数的图象上,根据平移求出即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB∥CD,CE、BE的交点为E,现作如下操作:
第一次操作,分别作∠ABE和∠DCE的平分线,交点为E1,
第二次操作,分别作∠ABE1和∠DCE1的平分线,交点为E2,
第三次操作,分别作∠ABE2和∠DCE2的平分线,交点为E3,…,
第n次操作,分别作∠ABEn﹣1和∠DCEn﹣1的平分线,交点为En.
若∠En=1度,那∠BEC等于 度

-
科目: 来源: 题型:
查看答案和解析>>【题目】校车安全是近几年社会关注的重大问题,安全隐患主要是超速和超载.某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点C,再在笔直的车道L上确定点D,使CD与L垂直,测得CD的长等于24米,在L上点D的同侧取点A、B,使∠CAD=30°,∠CBD=60°.

(1)求AB的长(结果保留根号);
(2)已知本路段对校车限速为45千米/小时,若测得某辆校车从A到B用时2秒,这辆校车是否超速?说明理由.(参考数据: ≈1.73,
≈1.73,  ≈1.41)
≈1.41) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,AB是⊙O的直径,AC切⊙O于点A,且AC=AB,CO交⊙O于点P,CO的延长线交⊙O于点F,BP的延长线交AC于点E,连接AP、AF.

求证:
(1)AF∥BE;
(2)△ACP∽△FCA;
(3)CP=AE. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线经过点A(﹣3,0),F(8,0),B(0,4)三点

(1)求抛物线解析式及对称轴;
(2)若点D在线段FB上运动(不与F,B重合),过点D作DC⊥轴于点C(x,0),将△FCD沿CD向左翻折,点B对应点为点E,△CDE与△FBO重叠部分面积为S.
①试求出S与x之间的函数关系式,并写出自变量取值范围.
②是否存在这样的点C,使得△BDE为直角三角形,若存在,求出C点坐标,若不存在,请说明理由;
(3)抛物线对称轴上有一点M,平面内有一点N,若以A,B,M,N四点组成的四边形为菱形,求点N的坐标. -
科目: 来源: 题型:
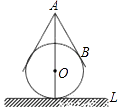
查看答案和解析>>【题目】用一个直径为10cm的玻璃球和一个圆锥形的牛皮纸纸帽制作一个不倒翁玩具,不倒翁的轴截面如图所示,圆锥的母线AB与⊙O相切于点B,不倒翁的顶点A到桌面L的最大距离是18cm.若将圆锥形纸帽表面全涂上颜色,则涂色部分的面积为cm2 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=4,BC=2,E是AB的中点,直线l平行于直线EC,且直线l与直线EC之间的距离为2,点F在矩形ABCD边上,将矩形ABCD沿直线EF折叠,使点A恰好落在直线l上,则DF的长为 .

相关试题

