【题目】已知抛物线经过点A(﹣3,0),F(8,0),B(0,4)三点
(1)求抛物线解析式及对称轴;
(2)若点D在线段FB上运动(不与F,B重合),过点D作DC⊥轴于点C(x,0),将△FCD沿CD向左翻折,点B对应点为点E,△CDE与△FBO重叠部分面积为S.
①试求出S与x之间的函数关系式,并写出自变量取值范围.
②是否存在这样的点C,使得△BDE为直角三角形,若存在,求出C点坐标,若不存在,请说明理由;
(3)抛物线对称轴上有一点M,平面内有一点N,若以A,B,M,N四点组成的四边形为菱形,求点N的坐标.
参考答案:
【答案】
(1)
解:设抛物线解析式为y=a(x+3)(x﹣8),
将点B(0,4)代入得4=a×(0+3)×(0﹣8),
解得a=﹣ ![]() .
.
故抛物线解析式为y=﹣ ![]() (x+3)(x﹣8),
(x+3)(x﹣8),
对称轴为x=(﹣3+8)÷2= ![]() ;
;
(2)
解:CE=CF=8﹣x,CD=4﹣ ![]() x,
x,
①当0<x<4时,
S= ![]() (8﹣x)(4﹣
(8﹣x)(4﹣ ![]() x)×[1﹣(
x)×[1﹣( ![]() )2]=﹣
)2]=﹣ ![]() x2+4x;
x2+4x;
当4≤x<8时,
S= ![]() (8﹣x)(4﹣
(8﹣x)(4﹣ ![]() x)=
x)= ![]() x2﹣4x+16;
x2﹣4x+16;
②分两种情况:当∠BED=90°时,△BOE∽△ECD,
∴ ![]() =
= ![]() =2,
=2,
∴EC=3,
∴C1(5,0);
当∠EBD=90°时;
△EOB∽△BOF,
∴ ![]() =
= ![]() =2,
=2,
∴EO=2,
∴EC= ![]() =5,
=5,
∴C2(3,0);
(3)
解:①以AB为边,以B为圆心,AB为半径画圆交对称轴于M1,M2两点,
M1I= ![]() =
= ![]() ,
,
由BM1,平移至AN1得,N1(﹣ ![]() ,
, ![]() ),N2(﹣
),N2(﹣ ![]() ,﹣
,﹣ ![]() ),
),
以A为圆心,AB为半径画圆,此时与对称轴没有交点,故不存在;
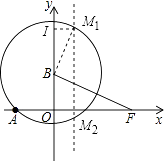
②以AB为对角线,直线AB的解析式为:y= ![]() x+4,
x+4,
则AB的中垂线MN的解析式为:y=﹣ ![]() x+
x+ ![]() ,
,
当x= ![]() 时,y=﹣1,
时,y=﹣1,
∴M( ![]() ,﹣1),
,﹣1),
∴N3(﹣ ![]() ,5).
,5).
综上所述:N1(﹣ ![]() ,
, ![]() ),N2(﹣
),N2(﹣ ![]() ,﹣
,﹣ ![]() ),N3(﹣
),N3(﹣ ![]() ,5).
,5).
【解析】(1)可设抛物线解析式为y=a(x+3)(x﹣8),将点B(0,4)代入已知抛物线方程,解得a的值即可;(2)①分两种情况:0<x<4;4≤x<8;进行讨论可求S与x之间的函数关系式;②分两种情况:当∠BED=90°时;当∠EBD=90°时;进行讨论可求C点坐标;(3)分两种情况:①以AB为边,以B为圆心,AB为半径画圆交对称轴于M1 , M2两点;②以AB为对角线;进行讨论可求点N的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】校车安全是近几年社会关注的重大问题,安全隐患主要是超速和超载.某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点C,再在笔直的车道L上确定点D,使CD与L垂直,测得CD的长等于24米,在L上点D的同侧取点A、B,使∠CAD=30°,∠CBD=60°.

(1)求AB的长(结果保留根号);
(2)已知本路段对校车限速为45千米/小时,若测得某辆校车从A到B用时2秒,这辆校车是否超速?说明理由.(参考数据: ≈1.73,
≈1.73,  ≈1.41)
≈1.41) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,AB是⊙O的直径,AC切⊙O于点A,且AC=AB,CO交⊙O于点P,CO的延长线交⊙O于点F,BP的延长线交AC于点E,连接AP、AF.

求证:
(1)AF∥BE;
(2)△ACP∽△FCA;
(3)CP=AE. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=
 (k>0,x>0)的图象上,点D的坐标为(
(k>0,x>0)的图象上,点D的坐标为(  ,2).
,2).
(1)求k的值;
(2)若将菱形ABCD沿x轴正方向平移,当菱形的一个顶点恰好落在函数y= (k>0,x>0)的图象上时,求菱形ABCD平移的距离.
(k>0,x>0)的图象上时,求菱形ABCD平移的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】用一个直径为10cm的玻璃球和一个圆锥形的牛皮纸纸帽制作一个不倒翁玩具,不倒翁的轴截面如图所示,圆锥的母线AB与⊙O相切于点B,不倒翁的顶点A到桌面L的最大距离是18cm.若将圆锥形纸帽表面全涂上颜色,则涂色部分的面积为cm2 .
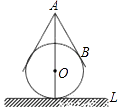
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=4,BC=2,E是AB的中点,直线l平行于直线EC,且直线l与直线EC之间的距离为2,点F在矩形ABCD边上,将矩形ABCD沿直线EF折叠,使点A恰好落在直线l上,则DF的长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组
 并在数轴上表示出它的解集.
并在数轴上表示出它的解集.
相关试题

