Question

【题目】如图，已知AB∥CD，CE、BE的交点为E，现作如下操作：

第一次操作，分别作∠ABE和∠DCE的平分线，交点为E1，

第二次操作，分别作∠ABE1和∠DCE1的平分线，交点为E2，

第三次操作，分别作∠ABE2和∠DCE2的平分线，交点为E3，…，

第n次操作，分别作∠ABEn﹣1和∠DCEn﹣1的平分线，交点为En．

若∠En=1度，那∠BEC等于　 　度

Answer 1

【答案】2n ．

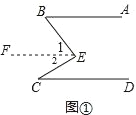
【解析】如图①，过E作EF∥AB，

∵AB∥CD，

∴AB∥EF∥CD，

∴∠B=∠1，∠C=∠2，

∵∠BEC=∠1+∠2，

∴∠BEC=∠ABE+∠DCE；

如图②，∵∠ABE和∠DCE的平分线交点为E1，

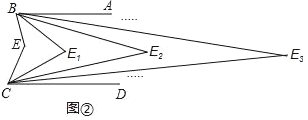
∴∠CE1B=∠ABE1+∠DCE1=∠ABE+∠DCE=∠BEC．

∵∠ABE1和∠DCE1的平分线交点为E2，

∴∠BE2C=∠ABE2+∠DCE2=∠ABE1+∠DCE1=∠CE1B=∠BEC；

如图②，∵∠ABE2和∠DCE2的平分线，交点为E3，

∴∠BE3C=∠ABE3+∠DCE3=∠ABE2+∠DCE2=∠CE2B=∠BEC；

…

以此类推，∠En=∠BEC．

∴当∠En=1度时，∠BEC等于2n度．

故答案为：2n ．