【题目】如图,矩形![]() 中,
中,![]() ,点
,点![]() 分别在
分别在![]() 上,且
上,且![]() .
.

(1)求证:四边形![]() 是菱形;
是菱形;
(2)求线段![]() 的长.
的长.
参考答案:
【答案】(1)见解析(2)![]()
【解析】
(1)根据矩形的性质得到CD=AB=8,AD=BC=4,CD∥AB,∠D=∠B=90°,求得CF=AE=83=5,根据勾股定理得到AF=CE=![]() =5,于是得到结论;
=5,于是得到结论;
(2)过F作FH⊥AB于H,得到四边形AHFD是矩形,根据矩形的性质得到AH=DF=3,FH=AD=4,根据勾股定理即可得到结论.
(1)证明:∵在矩形ABCD中,AB=8,BC=4,
∴CD=AB=8,AD=BC=4,CD∥AB,∠D=∠B=90°,
∵BE=DF=3,
∴CF=AE=83=5,
∴AF=CE=![]() =5,
=5,
∴AF=CF=CE=AE=5,
∴四边形AECF是菱形;
(2)解:过F作FH⊥AB于H,
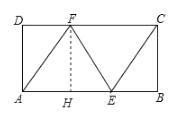
则四边形AHFD是矩形,
∴AH=DF=3,FH=AD=4,
∴EH=5-3=2,
∴EF=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1个单位长度的小正方形组成的网格中,点
 、
、 、
、 都是格点.
都是格点.
(1)将
 向左平移6个单位长度得到
向左平移6个单位长度得到 ;
;(2)将
 绕点
绕点 按逆时针方向旋转180°得到
按逆时针方向旋转180°得到 ,请画出
,请画出 ;
;(3)若点
 的坐标为(3,3);写出
的坐标为(3,3);写出 与
与 的对称中心的坐标_____.
的对称中心的坐标_____. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC在直角坐标系中,
(1)请写出△ABC各点的坐标.
(2)若把△ABC向上平移2个单位,再向左平移1个单位得到△A′B′C′,写出 A′、B′、C′的坐标,并在图中画出平移后图形.
(3)求出三角形ABC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某气球内充满了一定量的气体,当温度不变时,气球内气体的压强
 (kPa)是气体体积
(kPa)是气体体积 (m3)的反比例函数,其图像如图所示.
(m3)的反比例函数,其图像如图所示.
(1)求这个反比例函数的表达式;
(2)当气球内的体积为气体1.6m3时,求气体压强
 的值:
的值:(3)当气球内的气体压强大于150kPa时,气球将爆炸,为了安全起见,气体的体积不小于多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠ABD和∠BDC的平分线交于E,BE交CD于点F,∠1+∠2=90°.求证:

(1)AB∥CD;
(2)∠2+∠3=90°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
 中,函数
中,函数 的图像与函数
的图像与函数 (
( )的图像相交于点
)的图像相交于点 ,并与
,并与 轴交于点
轴交于点 .点
.点 是线段
是线段 上一点,
上一点, 与
与 的面积比为3:7.
的面积比为3:7.
(1)
 _____,
_____, _____.
_____.(2)求点
 的坐标;
的坐标;(3)若将
 绕点
绕点 逆时针旋转,得到
逆时针旋转,得到 ,其中点
,其中点 落在
落在 轴负半轴上,判断点
轴负半轴上,判断点 是否落在函数
是否落在函数 (
( )的图像上,并说明理由.
)的图像上,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小强从A处出发沿北偏东70°方向行走,走至B处,又沿着北偏西30°方向行走至C处,此时需把方向调整到与出发时一致,则方向的调整应是( )
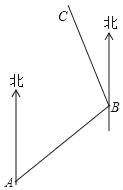
A. 左转 80° B. 右转80° C. 右转 100° D. 左转 100°
相关试题

